ECDSA and Bitcoin II: Base Point, Order and secp256k1

In previous post, we’ve got some general ideas about ECDSA, this post will focus on intuitions behind secp256k1, the set of parameters Bitcoin used. Before we dive in, we can get a glimpse of what it looks like(secp256k1.png).
More info: Recommended Elliptic Curve Domain Parameters: page 15.

I. Base point and order

1. Base point and it’s generated group

The example in previous post is : $a=1,b=1,P=23,x_{1}=3,y_{1}=10$. Or state in another away

$y^2=x^3+x+1\space mod\space 23$

We started from $G(0,1)$, a base point. By multiplying $G$ with $1,2,...,28$ respectivly, we generated a group of 28 points(the last point $\mathcal{O}$ is the point at infinity):$$(0, 1), (6, 19), (3, 13), (13, 16), (18, 3), (7, 11), (11, 3), (5, 19), (19, 18),$$

$(12, 4), (1, 16), (17, 20), (9, 16), (4, 0), (9, 7), (17, 3), (1, 7), (12, 19),$

$(19, 5), (5, 4), (11, 20), (7, 12), (18, 20), (13, 7), (3, 10), (6, 4), (0, 22)$

$\mathcal{O}$

If we starts from another point in the above group, we will see a very interesting property: the points generated by multiply this point are still in this group. Figure 3.1-3.27 show 27 base points and the group generated by them respectivly. One last base point does not show here is infinity point $\mathcal{O}$.By definition $\mathcal{O}+\mathcal{O}=\mathcal{O}$, the generated group of $\mathcal{O}$ consisits of one point: itself.

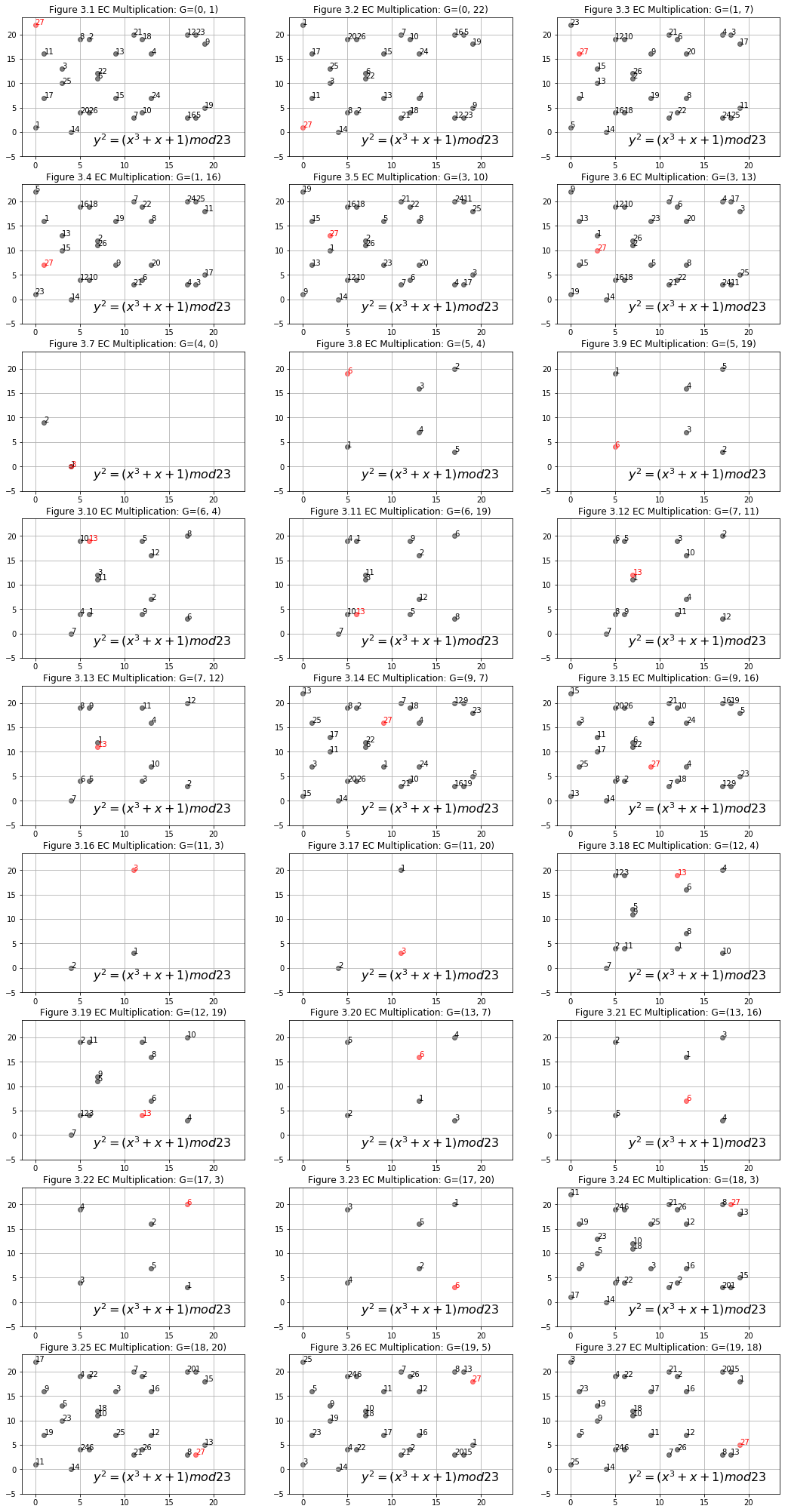
If we count the number of generated points of each group we will find another interesting property. There are 12 base points, each of them generates the same 28 points group(27 points + $\mathcal{O}$). There are 6 base points, each of them generates a group of 14 points. There are 6 other base points each of them genertates a group of 7 points. There are 3 base points each of them generates a group of 3 points. Point $\mathcal{O}$ generates a group of 1 point.

Base Point	# of Generated Points	Divisor of 28?
(0,1)(0,22)(1,7)(1,16)(3,10)(3,13)(9,7)(9,16)(18,3)(18,20)(19,5)(19,18)	28	yes
(6,4)(6,19)(7,11)(7,12)(12,4)(12,19)	14	yes
(5,4)(5,19)(13,7)(13,16)(17,3)(17,20)	7	yes
(4,0)(11,3)(11,20)	4	yes
$\mathcal{O}$	1	yes

The interesting property is: 28,14,7,4,1 are all divisors of 28. Is it a coincidence? No, it’s not. Before prove this property, let’s see where does this 28 come from.

2. The order of the curve

This 28 is called the order of the curve. It is determined by the elliptic curve $y^2=x^3+x+1$ and $mod\space 23$. Why? Let’s figure it out step by step.
First, $mod\space 23$ have 23 possible results:

$-1 \space mod \space 23 = 22$

$0 \space mod \space 23 = 0$

$1 \space mod \space 23 = 1$

$2 \space mod \space 23 = 2$

$...$

$22 \space mod \space 23 = 22$

$23 \space mod \space 23 = 0$

$24 \space mod \space 23 = 1$

$25 \space mod \space 23 = 2$

$...$

If $y$ is an integer, how many possible results $y^2 \space mod \space 23$ will have? Since in the ‘mod’ world only remainders matter, so it has at most 23 results. Actually, it’s far less than 23，since

$(23-y)^2 \space mod \space 23 = (\bcancel{23*23} - \bcancel{2*23*y} + y^2)\space mod \space 23= y^2 \space mod \space 23$

Specifically, there are 12 possible results:

$23^2 \space mod \space 23 = 0^2 \space mod \space 23 = 0 \space mod \space 23 = 0$

$22^2 \space mod \space 23 = 1^2 \space mod \space 23 = 1 \space mod \space 23 = 1$

$21^2 \space mod \space 23 = 2^2 \space mod \space 23 = 4 \space mod \space 23 = 4$

$20^2 \space mod \space 23 = 3^2 \space mod \space 23 = 9 \space mod \space 23 = 9$

$19^2 \space mod \space 23 = 4^2 \space mod \space 23 = 16 \space mod \space 23 = 16$

$18^2 \space mod \space 23 = 5^2 \space mod \space 23 = 25 \space mod \space 23 = 2$

$17^2 \space mod \space 23 = 6^2 \space mod \space 23 = 36 \space mod \space 23 = 13$

$16^2 \space mod \space 23 = 7^2 \space mod \space 23 = 49 \space mod \space 23 = 3$

$15^2 \space mod \space 23 = 8^2 \space mod \space 23 = 64 \space mod \space 23 = 18$

$14^2 \space mod \space 23 = 9^2 \space mod \space 23 = 81 \space mod \space 23 = 12$

$13^2 \space mod \space 23 = 10^2 \space mod \space 23 = 100 \space mod \space 23 = 8$

$12^2 \space mod \space 23 = 11^2 \space mod \space 23 = 121 \space mod \space 23 = 6$

How about $x^3+x+1 \space mod \space 23$? Still only remainders matter, so it has at most 23 results. Since $y^2=x^3+x+1\space mod\space 23$, we need to check whether these 23 results match the above 12 results.

$0^3+0+1 \space mod\space 23 = 1 \space mod\space 23 = 1 (match:\space y=1\space or\space y=22)$

$1^3+1+1 \space mod\space 23 = 3 \space mod\space 23 = 3 (match:\space y=7\space or\space y=16)$

$2^3+2+1 \space mod\space 23 = 11 \space mod\space 23 = 11 (no \space match)$

$3^3+3+1 \space mod\space 23 = 31 \space mod\space 23 = 8 (match:\space y=10\space or\space y=13)$

$4^3+4+1 \space mod\space 23 = 69 \space mod\space 23 = 0 (match:\space y=0)$

$5^3+5+1 \space mod\space 23 = 131 \space mod\space 23 = 16 (match:\space y=4\space or\space y=19)$

$6^3+6+1 \space mod\space 23 = 233 \space mod\space 23 = 16 (match:\space y=4\space or\space y=19)$

$7^3+7+1 \space mod\space 23 = 351 \space mod\space 23 = 6 (match:\space y=11\space or\space y=12)$

$8^3+8+1 \space mod\space 23 = 521 \space mod\space 23 = 15 (no \space match)$

$9^3+9+1 \space mod\space 23 = 739 \space mod\space 23 = 3 (match:\space y=7\space or\space y=16)$

$10^3+10+1 \space mod\space 23 = 1011 \space mod\space 23 = 22 (no \space match)$

$11^3+11+1 \space mod\space 23 = 1043 \space mod\space 23 = 9 (match:\space y=3\space or\space y=20)$

$12^3+12+1 \space mod\space 23 = 1741 \space mod\space 23 = 16 (match:\space y=4\space or\space y=19)$

$13^3+13+1 \space mod\space 23 = 2211 \space mod\space 23 = 3 (match:\space y=7\space or\space y=16)$

$14^3+14+1 \space mod\space 23 = 2759 \space mod\space 23 = 22 (no \space match)$

$15^3+15+1 \space mod\space 23 = 3391 \space mod\space 23 = 10 (no \space match)$

$16^3+16+1 \space mod\space 23 = 4113 \space mod\space 23 = 19 (no \space match)$

$17^3+17+1 \space mod\space 23 = 4931 \space mod\space 23 = 9 (match:\space y=3\space or\space y=20)$

$18^3+18+1 \space mod\space 23 = 5851 \space mod\space 23 = 9 (match:\space y=3\space or\space y=20)$

$19^3+19+1 \space mod\space 23 = 6879 \space mod\space 23 = 2 (match:\space y=5\space or\space y=18)$

$20^3+20+1 \space mod\space 23 = 8021 \space mod\space 23 = 17 (no \space match)$

$21^3+21+1 \space mod\space 23 = 9283 \space mod\space 23 = 14 (no \space match)$

$22^3+22+1 \space mod\space 23 = 10671 \space mod\space 23 = 22 (no \space match)$

There are 27 matched points:

$(0, 1), (0, 22), (1, 7), (1, 16), (3, 10), (3, 13), (4, 0), (5, 4), (5, 19),$

$(6, 4), (6, 19), (7, 11), (7, 12), (9, 7), (9, 16), (11, 3), (11, 20), (12, 4), (12, 19),$

$(13, 7), (13, 16), (17, 3), (17, 20), (18, 3), (18, 20), (19, 5), (19, 18)$

plus point $\mathcal{O}$, altogether 28 points. Use the same method, we can get the order of $y^2=x^3+x+1\space mod\space 37$ is 48 and the order of $y^2=x^3+x+1\space mod\space 487$ is 520, etc. Actually, there is a better method called Schoof Algorithm, with which we can get the order of the curve without go through every candidate points. In practice, such as Bitcoin, the order of the curve is very high. It’s impossible to go through every point. With Schoof Algorithm we can still get the order. You can find the Python code of Schoof Algorithm here. Try some small parameters youself.
Reference:
Elliptic Curve Cryptography

3. The order of a base point

The nubmer of points in the generated group of a base point is called the order of a base point. In the case of $y^2=x^3+x+1\space mod\space 23$, the order of each base point is a divisor of 28. For example, the order of (0,1) is 28 and the order of (6,4) is 14. Based on Lagrange’s theorem, we can prove that the order of a base point is a divisor of the order of the curve. Sometimes the order of the curve is a prime. And a prime has only two divisors: 1, and the prime itself. Therefore, except the order of point $\mathcal{O}$ is 1, the order of all other base points is equal to the order of the curve.

II. Parameters in secp256k1

1. The elliptic curve

In secp256k1, $a=0,b=7$. So the elliptic curve is

$y^2=x^3+7\space mod\space P$

where

$P = 2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 -1$

2. The order of the curve

In secp256k1, the order of the curve, denoted by $n$, is

$\text{FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141}$

in decimal, it’s

$115792089237316195423570985008687907852837564279074904382605163141518161494337$

3. Base point

In secp256k1, base point is $G(G_{x},G_{y})$, where

$G_{x}=79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798$

$G_{y}=483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8$

4. The order of the base point

We can verify the order of the curve $n$ is a prime, with the help of this Python code. Therefore, except the order of point $\mathcal{O}$ is 1, the order of all other base points, including G, is $n$.

5. Cofactor

By definition, cofactor

$h=\frac{the\space order\space of\space the\space curve}{the\space order\space of\space the\space base\space point}$

Obviousely, in secp256k1, $h=n/n=1$.