ECDSA and Bitcoin I: Intuition About Elliptic Curve

The set of parameters Bitcoin used is called secp256k1. It’s one of the Standards for Efficient Cryptogrpahy(SEC) or Standards for Efficient Cryptography Group (SECG). SEC or SECG is base on Elliptic Curve Digital Signature Algorithm(ECDSA). Before dive in, we can get a glimpse of what the algorithm looks like in Brown et al’s publication(ec1.png, ec2.png).
More info: Elliptic Curve Cryptography: page 6-7

I. Intuition About Elliptic Curve: Basics

1. Double a point(Add a point to itself):

Let’s consider a elliptic curve $(EC)$:

$y^2 = x^3 + ax + b$

, mod(P) will be discussed latter.

There is a initial point $G(x_{1},y_{1})$ on $EC$, how to get $D = G + G$?

Draw a tangent line at $G$, and cross $EC$ at $C(x_{c},y_{c})$. The vertical line crosses $C$, will cross $EC$ at $D(x_{3},y_{3})$, which is the result $G+G$ by definition.

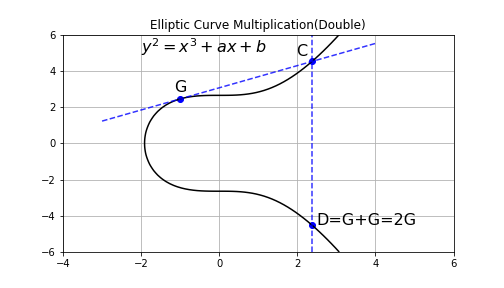
1.1 The slope of the tangent line:

$\because y^2 = x^3 + ax + b$

$\therefore 2ydy = (3x^2 +a)dx$

$\therefore {\frac{dy}{dx}} = {\frac{(3x^2 +a)}{2y}}$

$\therefore \lambda = {\frac{dy}{dx}} = {\frac{3x_{1}^2+a}{2y_{1}}}$

1.2 Point $C(x_{c},y_{c})$ :

$\because {\frac{y_{c}-y_{1}}{x_{c}-x_{1}}} = \lambda$

$\therefore y_{c}-y_{1} = \lambda(x_{c}-x_{1})$

$\therefore y_{c} = \lambda(x_{c}-x_{1}) + y_{1}$

$\because y^2 = x^3 + ax + b$

$\therefore y_{c}^2 = (\lambda(x_{c}-x_{1}) + y_{1})^2 = x_{c}^3 + ax_{c} + b$

$\therefore x_{c}^3 - (\lambda(x_{c}-x_{1}) + y_{1})^2 + ax_{c} + b = 0$

Let me put it another way:

$x^3 - (\lambda(x-x_{1}) + y_{1})^2 + ax + b = 0$

This equation has three roots, one of them is $x_{c}$.
What’s the other two roots? Yes, they are: $x_{1},x_{1}$(since tangent at $G(x_{1},y_{1})$).
Let’s focus on the coefficient of $x^2$:

$\because x^3 - (\lambda(x-x_{1}) + y_{1})^2 + ax + b = 0$

$... - \lambda^2x^2 + ... = 0$

the coefficient of $x^2$ is $\lambda^2$. On the other hand, since three roots are:$x_{1},x_{1},x_{c}$,

$(x-x_{1})(x-x_{1})(x-x_{c})=0$

$... - (x_{1}+x_{1}+x_{c})x^2 + ... = 0$

This two coefficient is identical, therefore

$\lambda^2=x_{1}+x_{1}+x_{c}$

$x_{c}=\lambda^2-x_{1}-x_{1}=\lambda^2-2x_{1}$

1.3 Point $D(x_{3},y_{3})$ :

$x_{3}=x_{c}=\lambda^2-x_{1}-x_{1}$

$y_{3}=-y_{c}= -(\lambda(x_{c}-x_{1}) + y_{1})=\lambda(x_{1}-x_{3}) - y_{1}$

where

$\lambda = {\frac{3x_{1}^2+a}{2y_{1}}}$

$G(x_{1},y_{1}) + G(x_{1},y_{1})$:

$\lambda = {\frac{3x_{1}^2+a}{2y_{1}}}$

$x_{3}=\lambda^2-x_{1}-x_{1}$

$y_{3}=\lambda(x_{1}-x_{3}) - y_{1}$

$D(x_{3},y_{3})=G+G$

2. Addition(Add two points together):

There are two initial points $A(x_{1},y_{1})$ and $B(x_{2},y_{2})$ on $EC$, how to get $D = A + B$?

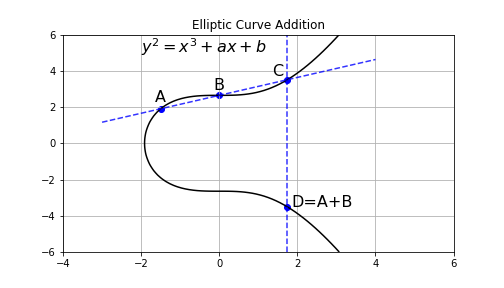
Draw a line through $A$ and $B$, and cross $EC$ at $C(x_{c},y_{c})$. The vertical line crosses $C$, will cross $EC$ at $D(x_{3},y_{3})$, which is the result $A+B$ by definition. If $A$ and $B$ are on the same vertical line, i.e. $x_{1}=x_{2},y_{1}=-y_{2}$, then $A+B=\mathcal{O}$, where $\mathcal{O}$ is an infinity point with the following properties(by definition):

$G+\mathcal{O}=\mathcal{O},\mathcal{O}+\mathcal{O}=\mathcal{O}$

Intuitively, $\mathcal{O}$ is a point faaaar away.

2.1 The slope of the line is determined by two initial points :

$\lambda = {\frac{dy}{dx}} = {\frac{y_{2}-y_{1}}{x_{2}-x_{1}}}$

2.2 Point $C(x_{c},y_{c})$:

$\because {\frac{y_{c}-y_{1}}{x_{c}-x_{1}}} = \lambda$

$\therefore y_{c}-y_{1} = \lambda(x_{c}-x_{1})$

$\therefore y_{c} = \lambda(x_{c}-x_{1}) + y_{1}$

$\because y^2 = x^3 + ax + b$

$\therefore y_{c}^2 = (\lambda(x_{c}-x_{1}) + y_{1})^2 = x_{c}^3 + ax_{c} + b$

$\therefore x_{c}^3 - (\lambda(x_{c}-x_{1}) + y_{1})^2 + ax_{c} + b = 0$

Let me put it another way:

$x^3 - (\lambda(x-x_{1}) + y_{1})^2 + ax + b = 0$

This equation has three roots, one of them is $x_{c}$.
What’s the other two roots? Yes, they are: $x_{1},x_{2}$.
Let’s focus on the coefficient of $x^2$:

$\because x^3 - (\lambda(x-x_{1}) + y_{1})^2 + ax + b = 0$

$... - \lambda^2x^2 + ... = 0$

the coefficient of $x^2$ is $\lambda^2$. On the other hand, since three roots are:$x_{1},x_{2},x_{c}$,

$(x-x_{1})(x-x_{2})(x-x_{c})=0$

$... - (x_{1}+x_{2}+x_{c})x^2 + ... = 0$

This two coefficient is identical, therefore

$\lambda^2=x_{1}+x_{2}+x_{c}$

$x_{c}=\lambda^2-x_{1}-x_{2}$

Reference: Explicit Addition Formulae

2.3 Point $D(x_{3},y_{3})$ :

$x_{3}=x_{c}=\lambda^2-x_{1}-x_{2}$

$y_{3}=-y_{c}= -(\lambda(x_{c}-x_{1}) + y_{1})= \lambda(x_{1}-x_{3}) - y_{1}$

where

$\lambda = {\frac{y_{2}-y_{1}}{x_{2}-x_{1}}}$

$A(x_{1},y_{1}) + B(x_{2},y_{2})$:

$\lambda = {\frac{y_{2}-y_{1}}{x_{2}-x_{1}}}$

$x_{3}=\lambda^2-x_{1}-x_{2}$

$y_{3}=\lambda(x_{1}-x_{3}) - y_{1}$

$D(x_{3},y_{3})=A+B$

II. Intuition About Elliptic Curve: mod

With mod, elliptic curve is no longer a curve, instead it is turned into a group of discrete points. With mod(P), the result D will be capped by P, therefore we can control the magnitude of the output.

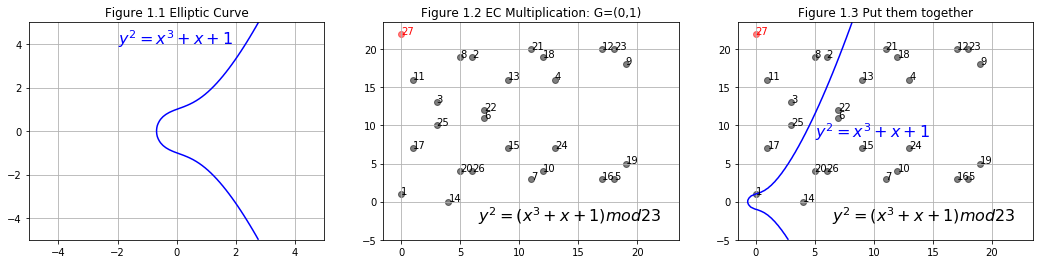
In Figure 1.2, we start from an initial point G(3,10), i.e. the point labeled 1, use EC multiplication and get the rest points in the group. EC multiplication, which is based on EC double and EC addition, will be discussed latter. Let's go over some details of `mod` first.

1. mod: Basics

Let’s see some examples:

$x \space mod \space P:$

$-1 \space mod \space 23 = 22$

$0 \space mod \space 23 = 0$

$1 \space mod \space 23 = 1$

$2 \space mod \space 23 = 2$

$...$

$22 \space mod \space 23 = 22$

$23 \space mod \space 23 = 0$

$24 \space mod \space 23 = 1$

$25 \space mod \space 23 = 2$

$...$

2. mod: Properties

$x+y \space mod \space P = (x \space mod \space P + y\space mod \space P)\space mod \space P$

$xy \space mod \space P = ((x \space mod \space P) (y\space mod \space P))\space mod \space P$

Why? Let’s see an example:

$x=25,y=30,P=23$

$25+30\space mod \space 23 = (23+2) +(23+7)\space mod \space 23=(\bcancel{23*2}+2+7)\space mod \space 23$

$=2+7\space mod \space 23=(25\space mod \space 23+30\space mod \space 23)\space mod \space 23$

Similarly,

$25*30\space mod \space 23 = (23+2) * (23+7)\space mod \space 23=(\bcancel{23*23}+\bcancel{23*2}+\bcancel{23*7}+2*7)\space mod \space 23$

$=2*7\space mod \space 23=(25\space mod \space 23*30\space mod \space 23)\space mod \space 23$

When mod, only remainders matter.

3. mod: Inverse

Sometimes, we need to caculate ${\frac{1}{A}}\space mod\space P$, i.e. modular inverse. As we know, if $A*B = 1$, $B$ is the inverse of $A$. The definition of modular inverses is similar.
If both $A\space and\space B$ are integers and $A*B\space mod \space P=1$, $B$ is the modular inverse of $A$. Or state in an other way: ${\frac{1}{A}}\space mod\space P=B$.

3.1 One Improtant Property

Note: If $A$ does not coprime to $P$, i.e. if $A$ shares at least one prime factor with $P$, $A$ has no modular inverse (mod $P$). This is why secp256k1 chooses a prime $P$, which we will discuss later.

An example:

$A=6, P=8(they\space share\space one\space prime\space factor\space 2)$

$6*0 \space mod \space 8=0=0*2$

$6*1 \space mod \space 8=2=1*2$

$6*2 \space mod \space 8=4=2*2$

$6*3 \space mod \space 8=2=1*2$

$6*4 \space mod \space 8=0=0*2$

$...$

A more general case:

$A=n*k, P=m*k(they\space share\space one\space prime\space factor\space k)$

$\because A*B=nB*k$

$\therefore A*B\space mod \space P=nB*k \space mod \space (m*k)$

The reault must be something like $t*k$, where $t$ is an integer.

3.2 Calculate Modular Inverses

If $A$ coprimes to $P$, how to find it’s modular inverse $B$? We can use Extend Euclidean Algorithm.

• An example ($A=7,P=23$):

			n	R	$\times$ 23	$\times$ 7	t
		23=1*23+0		23	$\color{green} 1$	$\color{green} 0$	0
		7=0+1*7		7	$\color{orange} 0$	$\color{orange} 1$	1
23=3*7+2	or	2=23- $\color{magenta} 3$*7	$\color{magenta} 3$	2	$\color{green} 1$- $\color{magenta} 3$* $\color{orange} 0$= $\color{blue} 1$	$\color{green} 0$- $\color{magenta} 3$* $\color{orange} 1$= $\color{blue} -3$	2
7=3*2+1	or	1=7- $\color{red} 3$*2	$\color{red} 3$	1	$\color{orange} 0$- $\color{red} 3$* $\color{blue} 1$=-3	$\color{orange} 1$- $\color{red} 3$*( $\color{blue} -3$)=10	3

From the last line of the above table, we have

$1=(-3) * 23 + 10 * 7$

$\therefore 10 * 7 = 3 * 23 +1$

$\therefore 10 * 7\space mod\space 23 = 1$

$\therefore B=10$

• General cases(it’s a loop until R=1 therefore $B=a_{t}$):

	n	R	$\times$P	$\times$A	t
$R_{0}$=1*$P$+0		$R_{0}=P$	$\color{green}p_{0}=1$	$\color{green}a_{0}=0$	0
$R_{1}$=0+1*$A$		$R_{1}=A$	$\color{orange}p_{1}=0$	$\color{orange}a_{1}=1$	1
$R_{2}=R_{0}$- $\color{magenta}n_{2}$*$R_{1}$	$\color{magenta}n_{2}$	$R_{2}$	$\color{green} p_{0}$- $\color{magenta}n_{2}$* $\color{orange}p_{1}$= $\color{blue}p_{2}$	$\color{green}a_{0}$- $\color{magenta}n_{2}$* $\color{orange}a_{1}$= $\color{blue}a_{2}$	2
…	…	…	…	…	…
1=$R_{t-2}$- $\color{red}n_{t}$*$R_{t-1}$	$\color{red}n_{t}$	1	$\color{orange}p_{t-2}$- $\color{red}n_{t}$* $\color{blue}p_{t-1}$=$p_{t}$	$\color{orange}a_{t-2}$- $\color{red}n_{t}$*( $\color{blue}a_{t-1}$)=$a_{t}$	t

JavaScript:

Python:

Reference: Modular inverses, Extend Euclidean Algorithm, Elliptic Curve Cryptography, HTML, JavaScript, Python

4. mod: Elliptic Curve

Recall: We need to caculate $\lambda$, $x_{3}$ and $y_{3}$. This time let’s put $mod P$ at the end of $x_{3}$ and $y_{3}$

4.1 Double a point(Add a point to itself)

From initial point $G(x_{1},y_{1})$:

$\lambda = {\frac{3x_{1}^2+a}{2y_{1}}}$

$x_{3}=\lambda^2-x_{1}-x_{1}\color{blue}\space mod\space P$

$y_{3}=\lambda(x_{1}-x_{3}) - y_{1}\color{blue}\space mod\space P$

$D(x_{3},y_{3})=G+G$

Based on the properties of mod and modular inverse,

$x_{3}=(\lambda^2{\color{blue}\space mod\space P}-x_{1}{\color{blue}\space mod\space P}-x_{1}{\color{blue}\space mod\space P})\color{blue}\space mod\space P$

$x_{3}=(\lambda{\color{blue}\space mod\space P} * \lambda{\color{blue}\space mod\space P}-x_{1}{\color{blue}\space mod\space P}-x_{1}{\color{blue}\space mod\space P})\color{blue}\space mod\space P$

Or,

$x_{3}=(\lambda{\color{blue}\space mod\space P} * \lambda{\color{blue}\space mod\space P}-x_{1}-x_{1})\color{blue}\space mod\space P$

Where,

$\lambda{\color{blue}\space mod\space P} = {\frac{3x_{1}^2+a}{2y_{1}}}{\color{blue}\space mod\space P} = ((3x_{1}^2+a){\color{blue}\space mod\space P} * {\frac{1}{2y_{1}}}{\color{blue}\space mod\space P})\color{blue}\space mod\space P$

$= ((3x_{1}^2+a){\color{blue}\space mod\space P} * 2y_{1}{\color{blue}\space inverse\space mod\space P})\color{blue}\space mod\space P$

And,

$y_{3}=(\lambda{\color{blue}\space mod\space P} * (x_{1}-x_{3}) - y_{1})\color{blue}\space mod\space P$

Python:

4.2 Addition

From initial points $A(x_{1},y_{1})$ and $B(x_{2},y_{2})$:

$\lambda{\color{blue}\space mod\space P} = {\frac{y_{2}-y_{1}}{x_{2}-x_{1}}}{\color{blue}\space mod\space P} = ((y_{2}-y_{1}){\color{blue}\space mod\space P} * {\frac{1}{x_{2}-x_{1}}}{\color{blue}\space mod\space P}){\color{blue}\space mod\space P}$

$= ((y_{2}-y_{1}){\color{blue}\space mod\space P} * (x_{2}-x_{1}) {\color{blue}\space inverse\space mod\space P}){\color{blue}\space mod\space P}$

And

$x_{3}=(\lambda{\color{blue}\space mod\space P} * \lambda{\color{blue}\space mod\space P}-x_{1}-x_{2})\color{blue} \space mod\space P$

$y_{3}=(\lambda{\color{blue}\space mod\space P} * (x_{1}-x_{3}) - y_{1}) \color{blue} \space mod\space P$

$D(x_{3},y_{3})=A+B$

Python code:

4.3 Multiplication

Multiplication, or scalar multiplication, is defined as add a point to itself many times. From a initial point $G(x_{1},y_{1})$:

$2*G = G+G$

$3*G = G+G+G$

$...$

$N*G = \underbrace{G+G+...+G}_{\text{N}}$

In practice, N is usually very large, say

$\text{FFFFFFFFFFFFFFFFFFFFFFFFFFFFFB673C211660358AAD66B17B368CD0364141}$

In decimal, it’s

$115792089237316195423570985008687907452837564279074904382605163141518161494337$

If we use the above method to calculate N*G, it will take a looooong time to get the result. How long specifically? Let’s estimate it. At the end of 2018, multi-core GHz processors are capable of processing over 100 billion instructions per second. There are about 4.2 billion active internet users around the world. Our unverse is around 13.8 billion years old. Even if all active internet users work together since the birth of the universe, until now we’ve only finished

$\frac{1}{2.6606833790440597\times 10^{47}}$

Fortunatly, we have another alternative method:

$2G = G+G$

$4G = 2G+2G$

$2^{3}G = 2^{2}G+2^{2}G$

$...$

$2^{m_{0}+m_{1}+...+m_{n}} * G = 2^{m_{0}}G+2^{m_{1}}G+...+2^{m_{n}}G$

$...$

In binary, $N$ is

$\underbrace{1111111111...0101000001}_{\text{256}}$

So,

$N=2^{256}+2^{255}+...+2^{9}+2^{7}+1$

Actually, if we are going to use this method, we still need to prove $+$ is associative, since $+$ is not ordinary plus it’s one dot on eclliptic curve plus another dot. It’s a little bit tricky here, let me show you an example:
How to prove the associativity? Silverman and Tate offered us a geometric proof in their textbook Rational Points on Elliptic Curves. The proof is very elegant, so I quoted it here.

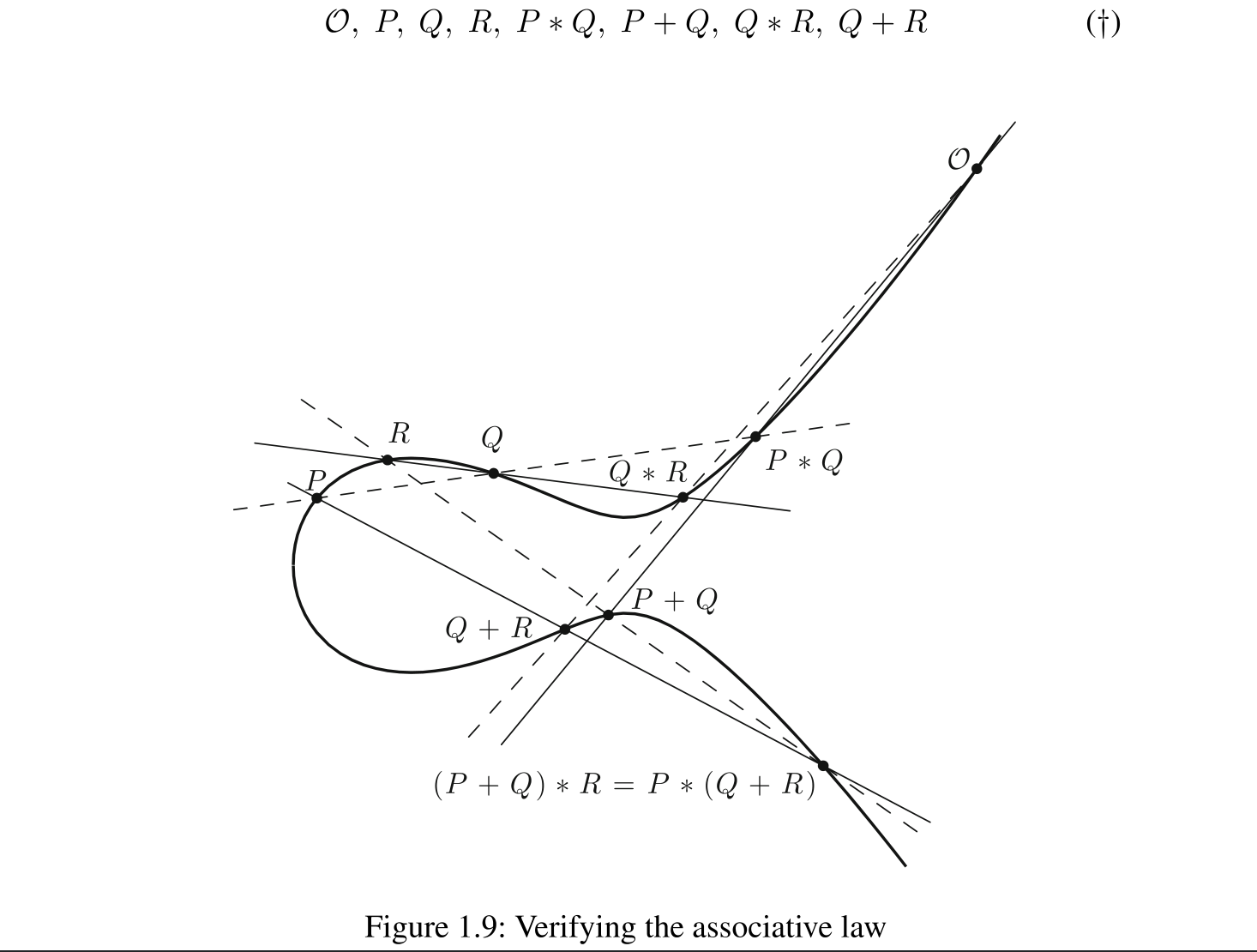
Python code(binary method):

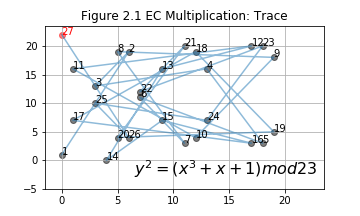
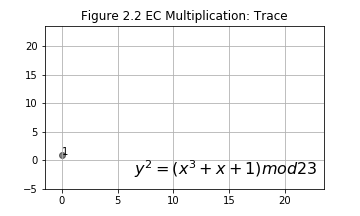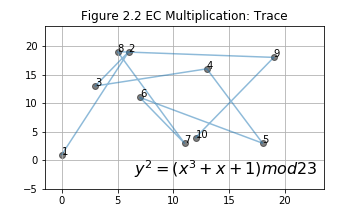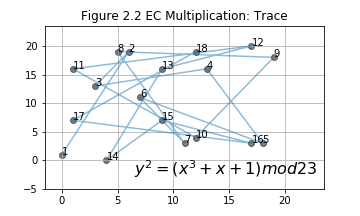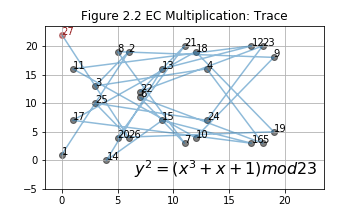
• An example: $a=1,b=1,P=23,x_{1}=3,y_{1}=10$.
  The initial point $G(0,1)$ is a generating point. $1*G,2*G,...,27*G$ are labeled in Figure 2.1. Notice, point 27 is right above point 1. Recall EC addition, what will happen if $A$ and $B$ are on the same vertical line? $A+B=\mathcal{O}$. That is to say, infinit point $\mathcal{O}$ is 28th point in this group genrated by $G$. Actually, this group only have 28 points and they can all be generated by multiply $G$ with $1,2,...,28$. More details will be discussed in the next section.

Reference: Elliptic Curve Cryptography, Python 2.7 Code