Notes for QUANTUM COMPUTING: Chp #2 Single-Qubit Quantum Systems

This is my notes for a highly recommended book “QUANTUM COMPUTING: A Gentle Introduction” by Eleanor Rieffel and Wolfgang Polak. The colored blocks in this notes are my interpretations, questions and answers to the exercises.

All theory is gray, my friend. But forever green is the tree of life.
Grau, teurer Freund, ist alle Theorie und grün des Lebens goldner Baum.

Johann Wolfgang von GoetheFaust: First Part

2.1 The Quantum Mechanics of Photon Polarization

2.1.1 A Simple Experiment

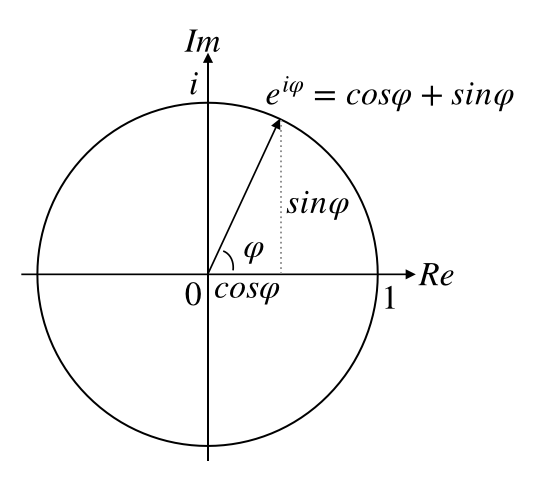
Figure 2.1, Figure 2.2, Figure 2.3

2.1.2 A Quantum Explanantion

Question 2.1

What is the classical explanantion of the experiment in term of waves?

• When $a$ and $b$ are both non-zero, $|v⟩ = a\lvert↑⟩ + b\lvert→⟩$ is said to be a superposition of $\lvert↑⟩$ and $\lvert→⟩$.
• When a photon with polarization $\lvert v⟩ = a\lvert↑⟩ + b\lvert→⟩$ meets a polaroid with preferred axis $\lvert↑⟩$, the photon will get through with probability $|a|^2$ and will be absorbed with probability $|b|^2$; the probability that a photon passes through the polaroid is the square of the magnitude of the amplitude of its polarization in the direction of the polaroid’s preferred axis.

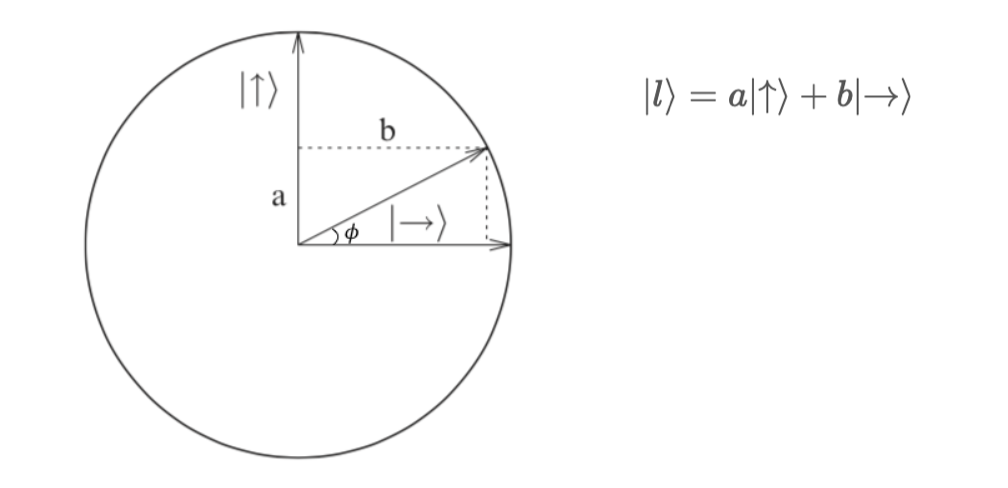
2.2 Single Quantum bits

• The space of possible polarization states of a photon is an example of a quantum bit, or qubit. A qubit has a continuum of possible values: any state represented by a unit vector $a\lvert↑⟩ + b\lvert→⟩$ is a legitimate qubit value. The amplitudes a and b can be complex numbers.

Question 2.2

In the photon polarization case, the imaginary coefficients correspond to circular polarization. What does this mean?

• Any quantum mechanical system that can be modeled by a two-dimensional complex vector space can be viewed as a qubit.
• Any vector multiplied by a modulus one [unit length] complex number represents the same quantum state.
• Dirac’s bra/ket notation:
  A $ket$ $\lvert v⟩=a_1\lvert\beta_1⟩+a_2\lvert\beta_2⟩+...+a_n\lvert\beta_n⟩$ can be written as $\begin{pmatrix}a_1\\a_2\\ \vdots\\a_n \end{pmatrix}$. The conjugate transpose of a ket $|v⟩$ is called a $bra$ $⟨v|=(\bar a_1, \bar a_2, ..., \bar a_n)$. If $\lvert u⟩=b_1\lvert\beta_1⟩+b_2\lvert\beta_2⟩+...+b_n\lvert\beta_n⟩$, the $braket$
  $⟨v|u⟩=⟨v||u⟩=(\bar a_1, \bar a_2, ..., \bar a_n)\begin{pmatrix}b_1\\b_2\\ \vdots\\b_n \end{pmatrix} =\displaystyle\sum_{i=1}^n\bar a_ib_i$.
• $B={\lvert\beta_1⟩, \lvert\beta_2⟩, ..., \lvert\beta_n⟩}$ is $orthonormal$ if $⟨\beta_i|\beta_j⟩=\delta_{ij}=\begin{cases} 1 &\text{if } i=j\\ 0 &\text{otherwise}\end{cases}$.
• In the standard basis, with ordering $\{\lvert0⟩, \lvert1⟩\}$, the basis elements $\lvert0⟩$ and $\lvert1⟩$ can be expressed as $\dbinom{1}{0}$ and $\dbinom{0}{1}$.
• Representing $|0⟩$ as $\dbinom{1}{0}$ and $|1⟩$ as $\dbinom{0}{1}$ or representing $|0⟩$ as $\frac{1}{\sqrt{2}}\dbinom{1}{-1}$ and $|1⟩$ as $\frac{1}{\sqrt{2}}\dbinom{1}{1}$ would be equally good as long as it is done consistently.
• Instead of qubits, physical systems with states modeled by three- or n-dimensional vector spaces could be used as fundamental units of computation. Three-valued units are called $qutrits$, and n-valued units are called qudits. Since qudits can be modeled using multiple $qubits$, a model of quantum information based on qudits has the same computational power as one based on qubits.

Question 2.3

How to model qudits using multiple qubits?

2.3 Single-Qubit Measurement

• Given a device for measuring the polarization of photons with associated basis $\{|u⟩, |u^\perp⟩\}$, the state $|v⟩ = a|u⟩ + b|u^\perp⟩$ is measured as $|u⟩$ with probability $|a|^2$ and as $|u^\perp⟩$ with probability $|b|^2$ .
  This is an axiom based on empirical observation.

Superposition

$Superposition$ is basis-dependent: all states are superpositions with respect to some bases and not with respect to others. For instance, $a\lvert0⟩ + b\lvert1⟩$ is a superposition with respect to the basis $\{|0⟩, |1⟩\}$ but not with respect to $\{a\lvert0⟩ + b\lvert1⟩, \bar b\lvert0⟩ - \bar a\lvert1⟩\}$.
It is okay to think of a superposition $|v⟩ = a\lvert0⟩ + b\lvert1⟩$ as in some sense being in both state $|0⟩$ and state $|1⟩$ at the same time, as long as that statement is not taken too literally: states that are combinations of $|0⟩$ and $|1⟩$ in similar proportions but with different amplitudes, such as $\frac{1}{\sqrt2}(|0⟩+|1⟩)$, $\frac{1}{\sqrt2}(|0⟩-|1⟩)$ and $\frac{1}{\sqrt2}(|0⟩-i|1⟩)$, represent distinct states that behave differently in many situations.

2.4 A Quantum Key Distribution Protocol

• Two general classes of keys exist: symmetric keys and public-private key pairs.
  Public-private key pairs consist of a public key, knowable by all, and a corresponding private key whose secrecy must be carefully guarded by the owner. Symmetric keys consist of a single key (or a pair of keys easily computable from one another) that are known to all of the legitimate parties and no one else.
• Quantum key distribution protocols establish a symmetric key between two parties, Alice and Bob.

BB84 (Charles Bennett and Gilles Brassard, 1984):

• The purpose is to establish a secret key, a random sequence of bit values 0 and 1, known only to the two parties, Alice and Bob, who may use this key to support a cryptographic task such as exchanging secret messages or detecting tampering.
• Suppose Alice and Bob are connected by two public channels: an ordinary bidirectional classical channel and a unidirectional quantum channel. The quantum channel allows Alice to send a sequence of single qubits to Bob; in our case we suppose the qubits are encoded in the polarization states of individual photons. Both channels can be observed by an eavesdropper Eve.
• The process:
  $Step\ 1:$ Alice generates a random sequence of classical bit values. For each bit of this sequence, Alice randomly chooses one of the following two agreed-upon bases and encodes it in the polarization state of a photon.
    * The standard basis: $0 \mapsto \lvert↑⟩, 1 \mapsto \lvert→⟩$.
    * The Hadamard basis: $0 \mapsto \lvert↗⟩=\frac{1}{\sqrt{2}}(\lvert↑⟩ + \lvert→⟩), 1 \mapsto \lvert↖⟩=\frac{1}{\sqrt{2}}(\lvert↑⟩ - \lvert→⟩)$.
  $Step\ 2:$ Alice sends this sequence of photons to Bob through the quantum channel.
  $Step\ 3:$ For each photon received, Bob randomly chooses one of the above two bases and measures the state.
  $Step\ 4:$ Over the classical channel, Alice and Bob check that Bob has received a photon for every one Alice has sent, and only then do Alice and Bob tell each other the bases they used for encoding and decoding (measuring) each bit. They discard all the bits on which their choice of bases differed.
  $Step\ 5:$ Depending on the level of assurance they require, Alice and Bob compare a certain number of bit values to check that no eavesdropping has occurred. These bits will also be discarded, and only the remaining bits will be used as their private key.
• man-in-the-middle attack: Eve impersonates Bob to Alice and impersonates Alice to Bob. To guard against such an attack, Alice and Bob need to combine it with an authentication protocol, recognizing each other’s voices or a more mathematical authentication protocol.

2.5 The State Space of a Single-Qubit System

The state space of a classical or quantum physical system is the set of all possible states of the system. Depending on which properties of the system are under consideration, a state of the system consists of any combination of the positions, momenta, polarizations, spins, energy, and so on of the particles in the system. The state space for a single qubit, no matter how it is realized, is the set of possible qubit values: $\{a\lvert0⟩ + b\lvert1⟩\}$, where $|a|^2+|b|^2=1$.

2.5.1 Relative Phases versus Global Phases

Question 2.5.1

$a\lvert0⟩ + b\lvert1⟩$ and $a'\lvert0⟩ + b'\lvert1⟩$ are considered the same qubit value if $a\lvert0⟩ + b\lvert1⟩ = c(a'\lvert0⟩ + b'\lvert1⟩)$ for some modulus one complex number $c$. Why?

To be explained

That the same quantum state is represented by more than one vector means that there is a critical distinction between the complex vector space in which we write our qubit values and the quantum state space itself.

• Equivalence relation $|v⟩ ∼ |v'⟩$ are used to indicate that $|v⟩ = c\lvert v'⟩$ for some complex $global\ phase$ $c = e^{i\phi_c}$. The space in which two two-dimensional complex vectors are considered equivalent if they are multiples of each other is called $complex\ projective\ space$ of dimension 1.
• This $quotient\ space$, a space obtained by identifying sets of equivalent vectors with a single point in the space, is expressed with the compact notation used for quotient spaces:

$\mathbf{CP}^1 =\{a\lvert0⟩+b\vert1⟩\}/∼$

• So the quantum state space for a single-qubit system is in one-to-one correspondence with the points of the complex projective space $\mathbf{CP}^1$.
• The $relative\ phase$ (in the standard basis) of a superposition $a\lvert0⟩ + b\lvert1⟩$ is the modulus one complex number $e^{iϕ_\alpha}$ satisfying $a/b = (|a|/|b|)e^{iϕ_\alpha}$. It’s a measure of the angle in the complex plane between the two complex numbers $a$ and $b$.

An interpretation

$Euler's\ formula:$

$e^{iφ}=\cosφ+i\sinφ$

where $φ$ is the angle in the complex plane.
In addition, complex numbers $b$ and $a$ can be represented by $|b|e^{iφ_b}$ and $|a|e^{iφ_a}$.
${\begin{array}{cc} b = |b|e^{iφ_b} \\ a = |a|e^{iφ_a} \\\end{array}}\Big\}\rArr \dfrac{b}{a}=\dfrac{|b|e^{iφ_b}}{|a|e^{iφ_a}}=\dfrac{|b|}{|a|}e^{i(φ_b-φ_a)}=\dfrac{|b|}{|a|}e^{iϕ_\alpha} \text{, where } ϕ_\alpha=φ_b-φ_a.$

• Therefore $ϕ_\alpha$ is the measure of the angle in the complex plane between $a$ and $b$.

Let’s come back to $global\ phase$ $c = e^{iφ_c}$. If $a'\lvert0⟩ + b'\lvert1⟩ = e^{iφ_c}(a\lvert0⟩ + b\lvert1⟩)$, and

$e^{iφ_c}(a\lvert0⟩ + b\lvert1⟩) = e^{iφ_c}(|a|e^{iφ_a}\lvert0⟩ + |b|e^{iφ_b}\lvert1⟩)=|a|e^{i(φ_a+φ_c)}\lvert0⟩ + |b|e^{i(φ_b+φ_c)}\lvert1⟩$

So $global\ phase$ $c = e^{iφ_c}$ means that both $a$ and $b$ add a same angle in the complex plane.

• $e^{iφ_c}(a\lvert0⟩ + b\lvert1⟩)$ and $a\lvert0⟩ + b\lvert1⟩$ represent the same quantum state means that $a$ and $b$ add a same angle $φ_c$ in the complex plane will not change the quantum state.

One more thing: inner product

Inner product $⟨a\vert b⟩=\bar ab=|a|e^{-iφ_a}|b|e^{iφ_b}=|a||b|e^{(iφ_b-iφ_a)}=|a||b|e^{iϕ_\alpha}$. Just like $reltive\ phase$, the angle of the inner product also measures the angle in the complex plane between $a$ and $b$.

Some useful single-qubit states

$|+⟩ =1/\sqrt{2}(|0⟩+|1⟩), \quad|i⟩ \hspace{0.7 em}= 1/\sqrt{2}(|0⟩ + i|1⟩)$

$|-⟩ =1/\sqrt{2}(|0⟩-|1⟩), \quad\lvert-i⟩ = 1/\sqrt{2}(|0⟩ - i|1⟩)$

The basis ${|+⟩, |-⟩}$ is referred to as the Hadamard basis. When discussing photon polarization, the notation ${|↖⟩, |↗⟩}$ is also used for the Hadamard basis.

• Some other books omit normalization factors, allowing vectors of any length to represent a state where two vectors represent the same state if they differ by any complex factor. This book explicitly writes the normalizations factors, both because then the amplitudes have a more direct relation to the measurement probabilities and because keeping track of the normalization factor provides a check that helps avoid errors.

2.5.2 Geometric Views of the State Space of a Single Qubit

• It is helpful to have models of the single-qubit state space in which there is a one-to-one correspondence between states and points in the space. These models are just different ways of looking at $complex\ projective\ space$ of dimension 1: the extended complex plane ($\mathbf{C} ∪ \{∞\}$) or a sphere.
• $Extended\ Complex\ Plane\ \mathbf{C} ∪ \{∞\}$ A correspondence between single-qubit states and the set of all complex numbers

$a\lvert0⟩+b\lvert1⟩\mapsto b/a=\alpha$

$\qquad$and it’s inverse

$\alpha \mapsto \frac{1}{\sqrt{1+|\alpha|^2}}\lvert0⟩+\frac{\alpha}{\sqrt{1+|\alpha|^2}}\lvert1⟩$

$(a=0,b=1)\rightleftarrows \alpha=∞$

$\qquad$Some examples:

$\lvert0⟩\mapsto 0,\enspace \quad \lvert+⟩\mapsto +1, \quad \lvert i⟩ \hspace{0.7 em}\mapsto +i$

$\lvert1⟩\mapsto \infin, \quad \lvert-⟩\mapsto -1, \quad \lvert -i⟩\mapsto -i$

• $Bloch\ Sphere$ A correspondence between complex number $\alpha=s+it$ and the point $(x,y,z)\in \mathbf{C}$ satisfying $|x|^2+|y|^2+|z|^2=1$, via the standard $stereographic\ projection$

$(s,t) \mapsto (x,y,z)=\left(\frac{2s}{1+|\alpha|^2}, \frac{2t}{1+|\alpha|^2}, \frac{1-|\alpha|^2}{1+|\alpha|^2}\right)$

$(x,y,z)\mapsto (s,t)=(\frac{x}{1+z}, \frac{y}{1+z})$

$\qquad$further requiring $\alpha=\infin \rightleftarrows (x,y,z)=(0,0,-1)$.

Stereographic projection and Bloch sphere

Stereographic projection is a particular mapping that projects a sphere onto a plane. Let’s assume the “south pole” is the projection point $P$ (See Figure I below). Now we need to project every point on the surface of the sphere to the “equatorial plane”. Let’s consider point $B=(x,y,z)$. The line pass through both $P$ and $B$ intercects the equatorial plane at point $A$. We say $A=(s,t,0)$ is $B$'s projection. Soon we will see $A=(\frac{x}{1+z}, \frac{y}{1+z}, 0)$.
In Figure I, there is a blue great circle passing through south pole, north pole and point $B$. Figure II is the plane of this great circle. Line $OAB'$ is part of the intercection of this plan and equatorial plan. Figure III is the equatorial plan.
In Figure II we have

$\frac{OA}{OB'}=\frac{OA}{CB}=\frac{PO}{PC}=\frac{1}{1+z}$

In Figure III we have

$\frac{s}{x}=\frac{t}{y}=\frac{OA}{OB'}=\frac{1}{1+z} \rArr (s,t)=(\frac{x}{1+z}, \frac{y}{1+z})$

This is $(x,y,z)\mapsto (s,t)$.

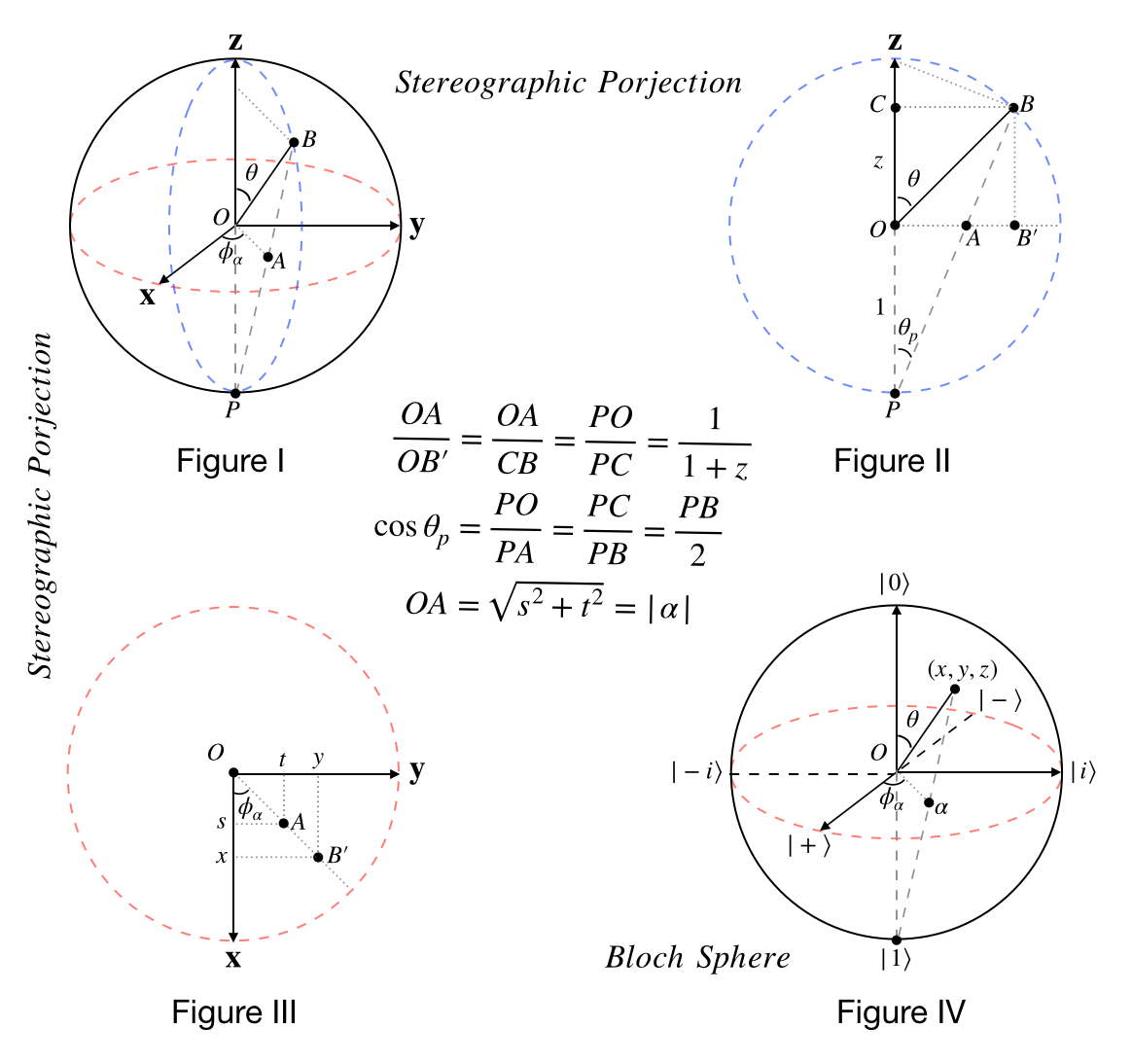
Let’s look at the opposite bidirection: $(s,t) \mapsto (x,y,z)$. Let’s say we have a complex number $\alpha=s+it$ and we want to project it to the unit sphere.
First, we put $\alpha$ on a Cartesian plane like Figure III and represented it as point $A=(s,t)$. (Obviously, $|\alpha|^2=s^2+t^2=OA^2$) Then we use this Cartesian plane as the equatorial plane of the unit sphere, as shown in Figure I. The line pass through both the south pole $P$ and point $A$ intercects the unit sphere at point $B=(x,y,z)$. As you can see, Figure I, II, III are the same. Again

$\frac{s}{x}=\frac{t}{y}=\frac{OA}{OB'}=\frac{1}{1+z} \rArr\begin{cases} x=(1+z)s\\ y=(1+z)t\\\end{cases}$

We still need to calculate $z$. From Figure II we have

$\cos\theta_p=\frac{PO}{PA}=\frac{PC}{PB} =\frac{PB}{2}$

here, “$2$” is the length of the diameter, from south pole ($P$) to north pole. Therefore

$(\frac{PO}{PA})^2=\frac{PC}{PB}\frac{PB}{2}=\frac{PC}{2}=\frac{1+z}{2}$

Since, $PO=1$ and $PA^2= PO^2+OA^2=1+|\alpha|^2$,

$\therefore \frac{1}{1+|\alpha|^2}=\frac{1+z}{2} \rArr 1+z=\frac{2}{1+|\alpha|^2} \rArr z=\frac{2}{1+|\alpha|^2}-1=\frac{1-|\alpha|^2}{1+|\alpha|^2}$

And

$1+z=\frac{2}{1+|\alpha|^2} \rArr\begin{cases} x=(1+z)s=\frac{2s}{1+|\alpha|^2}\\ y=(1+z)t=\frac{2t}{1+|\alpha|^2}\\\end{cases}$

$\therefore (x,y,z)=\left(\frac{2s}{1+|\alpha|^2}, \frac{2t}{1+|\alpha|^2}, \frac{1-|\alpha|^2}{1+|\alpha|^2}\right)$

By adding $\infin \mapsto (0,0,-1)$, every complex point can be projected on a unit sphere, the $Bloch\ sphere$. This is $(s,t) \mapsto (x,y,z)$.

$\qquad$Some useful points on Bloch sphere:

$\lvert0⟩\mapsto (0,0,+1), \quad \lvert+⟩\mapsto (+1,0,0), \quad \lvert i⟩ \hspace{0.7 em}\mapsto (0,+1,0)$

$\lvert1⟩\mapsto (0,0,-1), \quad \lvert-⟩\mapsto (-1,0,0), \quad \lvert -i⟩\mapsto (0,-1,0)$

Three representations of the quantum state space for a single-qubit system

Dirac $ket$ notation	Extended complex plane	Bloch sphere
$\begin{matrix} a\lvert0⟩ +b\lvert1⟩, \\ \vert a \vert^2+\vert b\vert^2=1 \end{matrix}$	$\alpha \in \mathbf{C} \cup \infin$	$(x,y,z)$ on the unit sphere
Not one-to-one	one-to-one	one-to-one

The relationship between Figure 2.4 (page 12) and Bloch shpere

It has been show that the angle $\phi_\alpha$ in the Bloch sphere is the same as the angle of $\alpha=s+it$ in the complex plane. Still another relationship needs to be clarified. In figure 2.4 (page 12), angle between $\vert0⟩$ and $\vert1⟩$ is $\pi/2$ while in Bloch sphere the angle between $\vert0⟩$ and $\vert1⟩$ is $\theta=\pi$. The latter is twice of the former. Why?
Recall what we have learned above

$\cos\theta_p=\frac{PO}{PA}=\frac{PO}{\sqrt{PO^2+OA^2}}=\frac{1}{\sqrt{1+|\alpha|^2}}$

For a vector $\vert v⟩= a\vert0⟩+b\vert1⟩$ in Figure 2.4, its corresponding complex number is $\alpha=b/a$. So

$|\alpha|=|b|/|a|\rArr \cos\theta_p=\frac{1}{\sqrt{1+(|b|/|a|)^2}}=\frac{|a|}{\sqrt{|a|^2+|b|^2}}$

In Figure 2.4, let’s name the angle between $\vert v⟩$ and $\vert 1⟩$, $\phi$. Obviously,

$\cos\phi=\frac{|a|}{\sqrt{|a|^2+|b|^2}}=\cos\theta_p$

$\therefore \cos\phi=\cos\theta_p\rArr \phi=\theta_p$

If we look closely, we will see that $\theta_p$ in Figure II is the angle between two lines: one is the line from the origin to $\vert1⟩$ and the other is from the projection point $P$ to $|v⟩$'s corresponding point on the Bloch sphere $(x,y,z)$. Intuitively, $\theta_p$ and $\phi$ are the same.
At last, $\theta$ in the Bloch sphere is twice of $\theta_p$.

$\therefore \theta=2\theta_p=2\phi$

2.5.3 Comments on General Quantum State Spaces

Question 2.5.3

• $Schr\ddot{o}dinger\ wave\ equation$ ?
• $Hilbert\ space$ ?

2.6 Reference

Three recommended books on quantum machanics:

• George Greenstein and Arthur G. Zajonc. The Quantum Challenge. Second Edition. Jones and Bartlett, 2006.
• Richard P. Feynman, Robert B. Leighton, and Matthew Sands. Lectures on Physics, Vol. III. New Millennium Edition. Basic Books, 2010.
• Ramamurti Shankar. Principles of Quantum Mechanics. 2nd ed. Plenum Press, 1980.

2.7 Exercises

2.7.1 Exercise 2.1

Let the direction $|v⟩$ of polaroid B’s preferred axis be given as a function of $θ$, $|v⟩ = \cosθ \lvert→⟩ + \sinθ\lvert↑⟩$, and suppose that the polaroids $A$ and $C$ remain horizontally and vertically polarized as in the experiment of Section 2.1.1. What fraction of photons reach the screen? Assume that each photon generated by the laser pointer has random polarization.

Answer 2.1

Let’s assume original light: $\lvert l⟩ = a\lvert↑⟩ + b\lvert→⟩$
Polaroid $A: \lvert→⟩$ with probability $|b|^{2}$
Polaroid $B: \lvert v⟩$ with probability $|b|^{2}\cos^{2}θ$

More Details 2.1

Step 1: Find a orthogonal state for $|v⟩$: $|v^\perp⟩ = \sinθ \lvert→⟩ - \cosθ\lvert↑⟩$
$\qquad$(How to find a orthogonal state will be shown in Exercise 2.7 and 2.14.)
Step 2: $\lvert→⟩=\cosθ \lvert v⟩ + \sinθ\lvert v^\perp⟩$
$\because \cosθ \lvert v⟩ + \sinθ\lvert v^\perp⟩=\cosθ (\cosθ \lvert→⟩ + \sinθ\lvert↑⟩) + \sinθ(\sinθ \lvert→⟩ - \cosθ\lvert↑⟩)$
$=\cos^{2}θ \lvert→⟩ + \cosθ\sinθ\lvert↑⟩ + \sin^{2}θ \lvert→⟩ - \sinθ\cosθ\lvert↑⟩=\cos^{2}θ \lvert→⟩ + \sin^{2}θ \lvert→⟩$
$=\lvert→⟩$

Polaroid $C: \lvert ↑⟩$ with probability $|b|^{2}\cos^{2}θ\sin^{2}θ$
If each photon generated by the laser pointer has random polarization, on average

$E(|b|^{2})=\frac{1}{2\pi}\int_0^{2\pi} \cos^2\phi\,d\phi=\frac{1}{2\pi}\int_0^{2\pi} \frac{1}{2}[1+\cos2\phi]\,d\phi=\frac{1}{2\pi}(\frac{1}{2}\phi+\frac{1}{4}\sin2\phi)\lvert_0^{2\pi}=\frac{1}{2}$

Therefore, the expected fraction of photons reach the screen will be

$\frac{1}{2}\cos^{2}θ\sin^{2}θ$

2.7.2 Exercise 2.2

Which pairs of expressions for quantum states represent the same state? For those pairs that represent different states, describe a measurement for which the probabilities of the two outcomes differ for the two states and give these probabilities.
a. $\lvert0⟩$ and $-\lvert0⟩$
b. $\lvert1⟩$ and $i\lvert1⟩$
c. $\frac{1}{\sqrt{2}}(\lvert0⟩ + \lvert1⟩)$ and $\frac{1}{\sqrt{2}}(-\lvert0⟩ + i\lvert1⟩)$
d. $\frac{1}{\sqrt{2}}(\lvert0⟩ + \lvert1⟩)$ and $\frac{1}{\sqrt{2}}(\lvert0⟩ - \lvert1⟩)$
e. $\frac{1}{\sqrt{2}}(\lvert0⟩ - \lvert1⟩)$ and $\frac{1}{\sqrt{2}}(\lvert1⟩ - \lvert0⟩)$
f. $\frac{1}{\sqrt{2}}(\lvert0⟩ + i\lvert1⟩)$ and $\frac{1}{\sqrt{2}}(i\lvert1⟩ - \lvert0⟩)$
g. $\frac{1}{\sqrt{2}}(\lvert+⟩ + \lvert-⟩)$ and $\lvert0⟩$
h. $\frac{1}{\sqrt{2}}(\lvert i⟩ - \lvert -i⟩)$ and $\lvert1⟩$
i. $\frac{1}{\sqrt{2}}(\lvert i⟩ + \lvert -i⟩)$ and √$\frac{1}{\sqrt{2}}(\lvert-⟩ + \lvert+⟩)$
j. $\frac{1}{\sqrt{2}}(\lvert0⟩ + e^{iπ/4}\lvert1⟩)$ and $\frac{1}{\sqrt{2}}(e^{-iπ/4}\lvert0⟩ + \lvert1⟩)$

Answer 2.2

In 2.5.1, we know that if $\lvert v⟩ = e^{i\phi}\lvert v'⟩$, $\lvert v⟩ \thicksim \lvert v'⟩$. And Euler equation tells us

$e^{i\phi}=\cos\phi+i\sin\phi$

Hence, if $\phi=\pi$, $e^{i\phi}=-1$; if $\phi=\frac{\pi}{2}$, $e^{i\phi}=i$.
a. $-\lvert0⟩=e^{i\pi}\lvert0⟩$; b. $i\lvert1⟩=e^{iπ/2}\lvert1⟩$; e. $\frac{1}{\sqrt{2}}(\lvert1⟩ - \lvert0⟩)=e^{i\pi}\frac{1}{\sqrt{2}}(\lvert0⟩ - \lvert1⟩)$
g. $\frac{1}{\sqrt{2}}(\lvert+⟩ + \lvert-⟩)=\frac{1}{\sqrt{2}}[\frac{1}{\sqrt{2}}(\lvert0⟩ + \lvert1⟩)+\frac{1}{\sqrt{2}}(\lvert0⟩-\lvert1⟩)]=\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}2\lvert0⟩=\lvert0⟩$
h. $\frac{1}{\sqrt{2}}(\lvert i⟩ - \lvert -i⟩)=\frac{1}{\sqrt{2}}[\frac{1}{\sqrt{2}}(\lvert0⟩ + i\lvert1⟩)-\frac{1}{\sqrt{2}}(\lvert0⟩ - i\lvert1⟩)] =\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}2i\lvert1⟩=i\lvert1⟩=e^{iπ/2}\lvert1⟩$
i. $\frac{1}{\sqrt{2}}(\lvert i⟩ + \lvert -i⟩)=\frac{1}{\sqrt{2}}[\frac{1}{\sqrt{2}}(\lvert0⟩ + i\lvert1⟩)+\frac{1}{\sqrt{2}}(\lvert0⟩ - i\lvert1⟩)]=\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}2\lvert0⟩=\lvert0⟩$
and $\frac{1}{\sqrt{2}}(\lvert+⟩ + \lvert-⟩)=\lvert0⟩$ (See g.)
j. $\frac{1}{\sqrt{2}}(e^{-iπ/4}\lvert0⟩ + \lvert1⟩)=e^{-iπ/4}[\frac{1}{\sqrt{2}}(\lvert0⟩ + e^{iπ/4}\lvert1⟩)]$

a,b,e,g,h,i,j are the pairs of expressions for quantum states represent the same state, while c,d,f are those pairs that represent different states.

c. $\frac{1}{\sqrt{2}}(\lvert0⟩ + \lvert1⟩)=\lvert+⟩$ and $\frac{1}{\sqrt{2}}(-\lvert0⟩ + i\lvert1⟩)=\frac{1}{2}[(-1+i)\lvert+⟩+(-1-i)\lvert-⟩]$.
Probabilities measured with basis $\{\lvert+⟩, \lvert-⟩\}$ are (1,0) and (1/2,1/2) respectively.

More Details 2.2

c. $\frac{1}{2}[(-1+i)\lvert+⟩+(-1-i)\lvert-⟩]$
$=\frac{1}{2\sqrt{2}}[(-1+i)(\lvert0⟩+\lvert1⟩)] + \frac{1}{2\sqrt{2}}[(-1-i)(\lvert0⟩-\lvert1⟩)]$
$=\frac{1}{2\sqrt{2}}(-2\lvert0⟩+2i\lvert1⟩)=\frac{1}{\sqrt{2}}(-\lvert0⟩+i\lvert1⟩)$

d. $\frac{1}{\sqrt{2}}(\lvert0⟩ + \lvert1⟩)=\lvert+⟩$ and $\frac{1}{\sqrt{2}}(\lvert0⟩ - \lvert1⟩) =\lvert-⟩$.
Probabilities measured with basis $\{\lvert+⟩, \lvert-⟩\}$ are (1,0) and (0,1) respectively.
f. $\frac{1}{\sqrt{2}}(\lvert0⟩ + i\lvert1⟩)=\lvert i⟩$ and $\frac{1}{\sqrt{2}}(i\lvert1⟩ - \lvert0⟩)=-\frac{1}{\sqrt{2}}(\lvert0⟩ - i\lvert1⟩)=-\lvert -i⟩=0\lvert i⟩-1\lvert -i⟩$.
Probabilities measured with basis $\{\lvert i⟩, \lvert -i⟩\}$ are (1,0) and (0,1) respectively.

2.7.3 Exercise 2.3

Which states are superpositions with respect to the standard basis, and which are not? For each state that is a superposition, give a basis with respect to which it is not a superposition.
a. $\lvert+⟩$
b. $\frac{1}{\sqrt{2}}(\lvert+⟩ + \lvert-⟩)$
c. $\frac{1}{\sqrt{2}}(\lvert+⟩ - \lvert-⟩)$
d. $\frac{\sqrt{3}}{2}\lvert+⟩ - \frac{1}{2}\lvert-⟩$
e. $\frac{1}{\sqrt{2}}(\lvert i⟩ - \lvert -i⟩)$
f. $\frac{1}{\sqrt{2}}(\lvert0⟩ - \lvert1⟩)$

Answer 2.3

a. $\lvert+⟩=\frac{1}{\sqrt{2}}(\lvert0⟩ + \lvert1⟩)$. Standard basis: superposition; basis $\{\lvert+⟩, \lvert-⟩\}$: deterministic.
b. $\frac{1}{\sqrt{2}}(\lvert+⟩ + \lvert-⟩)=\lvert0⟩$. Standard basis: deterministic.
c. $\frac{1}{\sqrt{2}}(\lvert+⟩ - \lvert-⟩)=\lvert1⟩$. Standard basis: deterministic.
d. $\frac{\sqrt{3}}{2}\lvert+⟩ - \frac{1}{2}\lvert-⟩=\frac{\sqrt{3}}{2}\frac{1}{\sqrt{2}}(\lvert0⟩ + \lvert1⟩) - \frac{1}{2}\frac{1}{\sqrt{2}}(\lvert0⟩ - \lvert1⟩)=\frac{\sqrt{3}-1}{2\sqrt{2}}\lvert0⟩ + \frac{\sqrt{3}+1}{2\sqrt{2}}\lvert1⟩$.
Standard basis: superposition; basis $\{\frac{\sqrt{3}}{2}\lvert+⟩ - \frac{1}{2}\lvert-⟩, \frac{1}{2}\lvert+⟩ + \frac{\sqrt{3}}{2}\lvert-⟩\}$: deterministic.
e. $\frac{1}{\sqrt{2}}(\lvert i⟩ - \lvert -i⟩)=i\lvert1⟩$. Standard basis: deterministic.
f. $\frac{1}{\sqrt{2}}(\lvert0⟩ - \lvert1⟩)=\lvert-⟩$. Standard basis: superposition; basis $\{\lvert+⟩, \lvert-⟩\}$: deterministic.

2.7.4 Exercise 2.4

Which of the states in 2.3 are superpositions with respect to the Hadamard basis, and which are not?

Answer 2.4

b,c,d,e are superpositions with respect to the Hadamard basis $\{\lvert+⟩, \lvert-⟩\}$.

More Details 2.4

e. $\frac{1}{\sqrt{2}}(\lvert i⟩ - \lvert -i⟩)=\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}2i\lvert1⟩=\frac{i}{\sqrt{2}}\frac{1}{\sqrt{2}}2\lvert1⟩=\frac{i}{\sqrt{2}}(\lvert+⟩ - \lvert-⟩)$

2.7.5 Exercise 2.5

Give the set of all values of $θ$ for which the following pairs of states are equivalent.
a. $\lvert1⟩$ and $\frac{1}{\sqrt{2}}(\lvert+⟩+e^{iθ}\lvert-⟩)$
b. $\frac{1}{\sqrt{2}}(\lvert i⟩+e^{iθ}\lvert -i⟩)$ and $\frac{1}{\sqrt{2}}(\lvert -i⟩+e^{-iθ}\lvert i⟩)$
c. $\frac{1}{2}\lvert0⟩ - \frac{\sqrt{3}}{2}\lvert1⟩$ and $e^{iθ}(\frac{1}{2}\lvert0⟩ - \frac{\sqrt{3}}{2}\lvert1⟩)$

Answer 2.5

a. $\lvert1⟩$ and $\frac{1}{\sqrt{2}}(\lvert+⟩+e^{iθ}\lvert-⟩)$. Not equivalent.
b. $\frac{1}{\sqrt{2}}(\lvert -i⟩+e^{-iθ}\lvert i⟩)=e^{-iθ}\frac{1}{\sqrt{2}}(e^{iθ}\lvert -i⟩+\lvert i⟩)=e^{-iθ}\frac{1}{\sqrt{2}}(\lvert i⟩+e^{iθ}\lvert -i⟩)$. Equivalent.
c. $\frac{1}{2}\lvert0⟩ - \frac{\sqrt{3}}{2}\lvert1⟩$ and $e^{iθ}(\frac{1}{2}\lvert0⟩ - \frac{\sqrt{3}}{2}\lvert1⟩)$. Equivalent.

2.7.6 Exercise 2.6

For each pair consisting of a state and a measurement basis, describe the possible measurement outcomes and give the probability for each outcome.
a. $\frac{\sqrt{3}}{2}\lvert0⟩ - \frac{1}{2}\lvert1⟩$, $\{\lvert0⟩, \lvert1⟩\}$
b. $\frac{\sqrt{3}}{2}\lvert1⟩ - \frac{1}{2}\lvert0⟩$, $\{\lvert0⟩, \lvert1⟩\}$
c. $\lvert -i⟩$, $\{\lvert0⟩, \lvert1⟩\}$
d. $\lvert 0⟩$, $\{\lvert+⟩, \lvert-⟩\}$
e. $\frac{1}{\sqrt{2}}(\lvert0⟩ - \lvert1⟩)$, $\{\lvert i⟩, \lvert -i⟩\}$
f. $\lvert 1⟩$, $\{\lvert i⟩, \lvert -i⟩\}$
g. $\lvert +⟩$, $\{\frac{1}{2}\lvert0⟩+\frac{\sqrt{3}}{2}\lvert1⟩, \frac{\sqrt{3}}{2}\lvert0⟩-\frac{1}{2}\lvert1⟩\}$

Answer 2.6

a. ($\frac{3}{4}, \frac{1}{4}$); b. ($\frac{1}{4}, \frac{3}{4}$); c. $\lvert -i⟩ =\frac{1}{\sqrt{2}}(\lvert0⟩ - i\lvert1⟩)$, ($\frac{1}{2}, \frac{1}{2}$); d. $\lvert 0⟩ =\frac{1}{\sqrt{2}}(\lvert+⟩ + \lvert-⟩)$, ($\frac{1}{2}, \frac{1}{2}$);
e. $\lvert-⟩ =\frac{1}{\sqrt{2}}(\lvert0⟩ - \lvert1⟩)=\frac{1}{2}[(1+i)\lvert i⟩+(1-i)\lvert-i⟩]$, ($\frac{1}{2}, \frac{1}{2}$);

More Details 2.6.1

e. $\frac{1}{2}[(1+i)\lvert i⟩+(1-i)\lvert-i⟩]$
$=\frac{1}{2\sqrt{2}}[(1+i)(\lvert0⟩+i\lvert1⟩)] + \frac{1}{2\sqrt{2}}[(1-i)(\lvert0⟩-i\lvert1⟩)]$
$=\frac{1}{2\sqrt{2}}(2\lvert0⟩+[(1+i)i-(1-i)i]\lvert1⟩)=\frac{1}{2\sqrt{2}}(2\lvert0⟩-2i\lvert1⟩)=\frac{1}{\sqrt{2}}(\lvert0⟩-i\lvert1⟩)=\lvert-⟩$
$|\frac{1}{2}(1+i)|^2=(\frac{1}{2}\sqrt{(1)^2+(1)^2})^2=(\frac{\sqrt{2}}{2})^2=\frac{2}{4}=\frac{1}{2}$
$|\frac{1}{2}(1-i)|^2=(\frac{1}{2}\sqrt{(1)^2+(-1)^2})^2=(\frac{\sqrt{2}}{2})^2=\frac{2}{4}=\frac{1}{2}$

f. $\lvert 1⟩=\frac{i}{\sqrt{2}}(\lvert i⟩ - \lvert -i⟩)$, ($\frac{1}{2}, \frac{1}{2}$);

More Details 2.6.2

f. $\frac{i}{\sqrt{2}}(\lvert i⟩ - \lvert -i⟩) =\frac{i}{\sqrt{2}}\frac{1}{\sqrt{2}}(-2i)\lvert1⟩=\lvert1⟩$, and $|\frac{i}{\sqrt{2}}|^2=|-\frac{i}{\sqrt{2}}|^2=\frac{1}{2}$

g. $\lvert +⟩=\frac{1}{\sqrt{2}}(\lvert 0⟩ + \lvert 1⟩) =\frac{1+\sqrt{3}}{2\sqrt{2}}(\frac{1}{2}\lvert0⟩+\frac{\sqrt{3}}{2}\lvert1⟩)+ \frac{\sqrt{3}-1}{2\sqrt{2}}(\frac{\sqrt{3}}{2}\lvert0⟩-\frac{1}{2}\lvert1⟩)$, $(\frac{4+2\sqrt{3}}{8},\frac{4-2\sqrt{3}}{8})$

More Details 2.6.3

g. $\frac{1}{2}(\frac{1}{2}\lvert0⟩+\frac{\sqrt{3}}{2}\lvert1⟩)+\frac{\sqrt{3}}{2}(\frac{\sqrt{3}}{2}\lvert0⟩-\frac{1}{2}\lvert1⟩)=\lvert0⟩$
$\quad\frac{\sqrt{3}}{2}(\frac{1}{2}\lvert0⟩+\frac{\sqrt{3}}{2}\lvert1⟩)-\frac{1}{2}(\frac{\sqrt{3}}{2}\lvert0⟩-\frac{1}{2}\lvert1⟩)=\lvert1⟩$
$\therefore\lvert +⟩=\frac{1}{\sqrt{2}}(\lvert 0⟩ + \lvert 1⟩) =\frac{1}{\sqrt{2}}[\frac{1}{2}(\frac{1}{2}\lvert0⟩+\frac{\sqrt{3}}{2}\lvert1⟩)+\frac{\sqrt{3}}{2}(\frac{\sqrt{3}}{2}\lvert0⟩-\frac{1}{2}\lvert1⟩)+\frac{\sqrt{3}}{2}(\frac{1}{2}\lvert0⟩+\frac{\sqrt{3}}{2}\lvert1⟩)-\frac{1}{2}(\frac{\sqrt{3}}{2}\lvert0⟩-\frac{1}{2}\lvert1⟩)] =\frac{1+\sqrt{3}}{2\sqrt{2}}(\frac{1}{2}\lvert0⟩+\frac{\sqrt{3}}{2}\lvert1⟩)+ \frac{\sqrt{3}-1}{2\sqrt{2}}(\frac{\sqrt{3}}{2}\lvert0⟩-\frac{1}{2}\lvert1⟩)$
And $|\frac{1+\sqrt{3}}{2\sqrt{2}}|^2=\frac{4+2\sqrt{3}}{8}$, $|\frac{\sqrt{3}-1}{2\sqrt{2}}|^2=\frac{4-2\sqrt{3}}{8}$

2.7.7 Exercise 2.7

For each of the following states, describe all orthonormal bases that include that state.
a. $\frac{1}{\sqrt{2}}(\lvert0⟩ + i\lvert1⟩)$
b. $\frac{1+i}{2}\lvert0⟩ - \frac{1-i}{2}\lvert1⟩$
c. $\frac{1}{\sqrt{2}}(\lvert0⟩ + e^{iπ/6}\lvert1⟩)$
d. $\frac{1}{2}\lvert+⟩ - \frac{i\sqrt{3}}{2}\lvert-⟩$

Answer 2.7

Assume $\lvert v⟩=a\lvert0⟩+b\lvert1⟩, \lvert u⟩=a_u\lvert0⟩+b_u\lvert1⟩$, $\{\lvert v⟩, \lvert u⟩\}$ is an orthogonal basis means that

$⟨v|u⟩=⟨v||u⟩=\begin{pmatrix}\bar{a} & \bar{b}\end{pmatrix}\begin{pmatrix}a_u \\ b_u\end{pmatrix}=\bar{a}a_u+\bar{b}b_u=0$

Obviously, we may choose $a_u=\bar{b}, b_u=-\bar{a}$.
Therefore, $\{a\lvert0⟩+b\lvert1⟩, \bar{b}\lvert0⟩-\bar{a}\lvert1⟩\}$ is an orthogonal basis, and $\{a\lvert0⟩+b\lvert1⟩, e^{i\phi}(\bar{b}\lvert0⟩-\bar{a}\lvert1⟩)\}$ are all orthogonal bases that include $\lvert v⟩$.
a. $\{\frac{1}{\sqrt{2}}(\lvert0⟩ + i\lvert1⟩), e^{i\phi}\frac{1}{\sqrt{2}}(-i\lvert0⟩ - \lvert1⟩)\}$ or $\{\lvert i⟩, e^{i\varphi}\lvert -i⟩\}$;

More Details 2.7

a. $e^{i\phi}\frac{1}{\sqrt{2}}(-i\lvert0⟩ - \lvert1⟩)=e^{i\phi}(-i)(\frac{1}{\sqrt{2}}(\lvert0⟩ - i\lvert1⟩))=e^{i\phi}e^{i\pi}\frac{1}{\sqrt{2}}(\lvert0⟩ - i\lvert1⟩)$
$\quad=e^{i(\phi+\frac{3\pi}{2})}\frac{1}{\sqrt{2}}(\lvert0⟩ - i\lvert1⟩) =e^{i\varphi}\frac{1}{\sqrt{2}}(\lvert0⟩ - i\lvert1⟩)$, where $\varphi=\phi+\frac{3\pi}{2}$
$\therefore$ $\{\frac{1}{\sqrt{2}}(\lvert0⟩ + i\lvert1⟩), e^{i\varphi}\frac{1}{\sqrt{2}}(\lvert0⟩ - i\lvert1⟩)\}$ =$\{\lvert i⟩, e^{i\varphi}\lvert -i⟩\}$ are also all orthogonal bases that include $\frac{1}{\sqrt{2}}(\lvert0⟩ + i\lvert1⟩)$.

b. $\{\frac{1+i}{2}\lvert0⟩ - \frac{1-i}{2}\lvert1⟩, e^{i\phi}(-\frac{1-i}{2}\lvert0⟩ - \frac{1+i}{2}\lvert1⟩)\}$ or $\{\frac{1+i}{2}\lvert0⟩ - \frac{1-i}{2}\lvert1⟩, e^{i\varphi}(\frac{1-i}{2}\lvert0⟩ + \frac{1+i}{2}\lvert1⟩)\}$
$\quad\varphi=\phi+\pi$;
c. $\{\frac{1}{\sqrt{2}}(\lvert0⟩ + e^{iπ/6}\lvert1⟩), e^{i\phi}(\frac{1}{\sqrt{2}}(e^{-iπ/6}\lvert0⟩ - \lvert1⟩))\}$ or
$\quad$$\{\frac{1}{\sqrt{2}}(\lvert0⟩ + e^{iπ/6}\lvert1⟩), e^{i\varphi}(\frac{1}{\sqrt{2}}(\lvert0⟩ - e^{iπ/6}\lvert1⟩))\}$, $\varphi=\phi-π/6$;
d. $\{\frac{1}{2}\lvert+⟩ - \frac{i\sqrt{3}}{2}\lvert-⟩, e^{i\phi}(\frac{i\sqrt{3}}{2}\lvert+⟩ - \frac{1}{2}\lvert-⟩)\}$

2.7.8 Exercise 2.8

Alice is confused. She understands that $\lvert1⟩$ and $-\lvert1⟩$ represent the same state. But she does not understand why that does not imply that $\frac{1}{\sqrt{2}}(\lvert0⟩+\lvert1⟩)$ and $\frac{1}{\sqrt{2}}(\lvert0⟩-\lvert1⟩)$ would be the same state. Can you help her out?

Answer 2.8

For $\lvert1⟩$ and $-\lvert1⟩$, $\alpha=b/a=1/0=\infin=-1/0$;
while for $\frac{1}{\sqrt{2}}(\lvert0⟩+\lvert1⟩)$ and $\frac{1}{\sqrt{2}}(\lvert0⟩-\lvert1⟩)$, $\alpha=b/a =\frac{1}{\sqrt{2}}/\frac{1}{\sqrt{2}}=1=\not-1=\frac{1}{\sqrt{2}}/(-\frac{1}{\sqrt{2}})$.

2.7.9 Exercise 2.9

In the BB84 protocol, how many bits do Alice and Bob need to compare to have a 90 percent chance of detecting Eve’s presence?

Answer 2.9

8 bits

More Details 2.9

Basis 1: $0 \mapsto \lvert↑⟩, 1 \mapsto \lvert→⟩$; Basis 2: $0 \mapsto \lvert↗⟩, 1 \mapsto \lvert↖⟩$.
Discarding all the bits on which Alice’s and Bob’s choice of bases difftered, let’s only consider the remaining bits. Suppose Alice’s information was 0 and she chose Basis 1.

• 1/2 chance: Eve chose Basis 1 and she got and sent Bob the correct photon $\lvert↑⟩$. Bob chose Basis 1 too and he measured the correct state $\lvert↑⟩$.
• 1/2 chance: Eve chose Basis 2 and she got and sent Bob $\lvert↗⟩$ or $\lvert↖⟩$ with half chance each. No matter $\lvert↗⟩$ or $\lvert↖⟩$, Bob chose Basis 1 too and he got half chance to get the correct state $\lvert↑⟩$.

Bob’s chance of getting the correct state is $\frac{1}{2}+\frac{1}{2}\times\frac{1}{2}=\frac{3}{4}$.
After comparing $n$ bits, the chance of detecting Eve’s presence is:

$p=1-(\frac{3}{4})^{n}$

When $n=8, p\approx0.9$.

2.7.10 Exercise 2.10

Analyze Eve’s success in eavesdropping on the BB84 protocol if she does not even know which two bases to choose from and so chooses a basis at random at each step.
a. Onaverage,what percentage of bit values of the final key will Eve know for sure after listening to Alice and Bob’s conversation on the public channel?
b. On average, what percentage of bits in her string are correct?
c. How many bits do Alice and Bob need to compare to have a 90 percent chance of detecting
Eve’s presence?

Answer 2.10

Suppose Eve chose a random basis $\{|v⟩, |v^\perp⟩\} = \{\sinθ\lvert↑⟩ + \cosθ\lvert→⟩, \cosθ\lvert↑⟩ - \sinθ \lvert→⟩\}$
a. 0.
Since Eve chose a random basis, Bob’s chance of deterministicly getting the correct state was negligible. Eve knew nothing for sure.
b. 1/2.
The chance of choosing basis $\{|v⟩, |v^\perp⟩\}$ is the same as choosing basis $\{|v^\perp⟩, |v⟩\}$. So the chance of getting $0$ is the same as getting $1$. On average, 50 percent of Eve’s string are correct. Only she doesn’t know which is correct which is not. It’s just like ramdom guess. You will have 50 percent of chance getting the correct number, but you don’t know when.
c. 8 bits.

More Details 2.10

Basis 1: $0 \mapsto \lvert↑⟩, 1 \mapsto \lvert→⟩$; Basis 2: $0 \mapsto \lvert↗⟩, 1 \mapsto \lvert↖⟩$.
Discarding all the bits on which Alice’s and Bob’s choice of bases difftered, let’s only consider the remaining bits. Suppose Alice’s information was 0 and she chose Basis 1.
$\because\sinθ|v⟩+\cosθ|v^\perp⟩=\sinθ(\sinθ\lvert↑⟩ + \cosθ\lvert→⟩)+\cosθ(\cosθ\lvert↑⟩ - \sinθ \lvert→⟩)$
$\quad=\sin^2θ\lvert↑⟩+\cos^2θ\lvert↑⟩=\lvert↑⟩$
$\therefore \lvert↑⟩= \sinθ|v⟩+\cosθ|v^\perp⟩$

• $\sin^2θ$ chance: Eve got and sent Bob $|v⟩$. Bob chose Basis 1 too and his chance of got the correct state $\lvert↑⟩$ is $\sin^2θ$.
• $\cos^2θ$ chance: Eve got and sent Bob $|v^\perp⟩$. Bob chose Basis 1 too and his chance of got the correct state $\lvert↑⟩$ is $\cos^2θ$.

Bob’s chance of getting the correct state is

$\sin^2θ\sin^2θ+\cos^2θ\cos^2θ=\sin^4θ+\cos^4θ$

On average,

$\frac{1}{2\pi}\int_0^{2\pi} (\sin^4θ+\cos^4θ)\,dθ=\frac{1}{2\pi}\int_0^{2\pi} (1-2\sin^2θ\cos^2θ)\,dθ$

$=1-\frac{1}{\pi}\int_0^{2\pi} \sin^2θ\cos^2θ\,dθ=1-\frac{1}{\pi}\int_0^{2\pi} \frac{1}{2}(1-\cos2θ) \frac{1}{2}(1+\cos2θ)\,dθ$

$=1-\frac{1}{4\pi}\int_0^{2\pi} (1-\cos^22θ)\,dθ=1-\frac{1}{4\pi}\int_0^{2\pi} \sin^22θ\,dθ$

$=1-\frac{1}{4\pi}\int_0^{2\pi} \frac{1}{2}(1-\cos4θ)\,dθ=1-\frac{1}{4}+\frac{1}{8\pi}\int_0^{2\pi} \cos4θ\,dθ$

$=\frac{3}{4}+\frac{1}{32\pi}\int_0^{2\pi} \cos4θ\,d4θ=\frac{3}{4}+\frac{1}{32\pi}\sin4θ\lvert_0^{2\pi}=\frac{3}{4}$

After comparing $n$ bits, the chance of detecting Eve’s presence is:

$p=1-(\frac{3}{4})^{n}$

When $n=8, p\approx0.9$.

2.7.11 Exercise 2.11

$B92$ quantum key distribution protocol. In 1992 Bennett proposed the following quantum key distribution protocol. Instead of encoding each bit in either the standard basis or the Hadamard basis as is done in the $BB84$ protocol, Alice encodes her random string $x$ as follows
$0 \mapsto \lvert0⟩$
$1 \mapsto \lvert+⟩=\frac{1}{\sqrt{2}}(\lvert0⟩+\lvert1⟩)$
and sends them to Bob. Bob generates a random bit string $y$. If $y_i = 0$ he measures the $i$ th qubit in the Hadamard basis $\{\lvert+⟩, \lvert-⟩\}$, if $y_i = 1$ he measures in the standard basis $\{\lvert0⟩, \lvert1⟩\}$. In this protocol, instead of telling Alice over the public classical channel which basis he used to measure each qubit, he tells her the results of his measurements. If his measurement resulted in $\lvert+⟩$ or $\lvert0⟩$ Bob sends $0$; if his measurement indicates the state is $\lvert1⟩$ or $\lvert-⟩$, he sends $1$. Alice and Bob discard all bits from strings $x$ and $y$ for which Bob’s bit value from measurement yielded $0$, obtaining strings $x'$ and $y'$. Alice uses $x'$ as the secret key and Bob uses $y'$. Then, depending on the security level they desire, they compare a number of bits to detect tampering. They discard these check bits from their key.
a. Show that if Bob receives exactly the states Alice sends, then the strings $x'$ and $y'$ are identical strings.
b. Why didn’t Alice and Bob decide to keep the bits of $x$ and $y$ for which Bob’s bit value from measurement was $0$?
c. What if an eavesdropper Eve measures each bit in either the standard basis or the Hadamard basis to obtain a bit string $z$ and forwards the measured qubits to Bob? On average, how many bits of Alice and Bob’s key does she know for sure after listening in on the public classical? If Alice and Bob compare $s$ bit values of their strings $x'$ and $y'$, how likely are they to detect Eve’s presence?

Answer 2.11

a. Assuming $x_i'=0$ and Alice sent $|0⟩$, Bob’s measurement indicates the state is either $\lvert1⟩$ or $\lvert-⟩$. $\lvert1⟩$ was impossible, no matter which basis Bob chose. It must be $\lvert-⟩$. That is to say, Bob chose the Hadamard basis and $y_i'=0$. Similarly, if $x_i'=1$, $y_i'=1$.
b. Assuming $x_i'=0$ and Alice sent $|0⟩$ and Bob’s bit value from measurement was $0$. Then Bob’s measurement indicates the state is either $\lvert0⟩$ or $\lvert+⟩$. That is to say, Bob chose the Hadamard basis and $y_i'=0$ or he chose the standard basis and $y_i'=1$. So when measurement was 0, Bob couldn’t be sure his measurement was correct or not.
c. On average, Eve knew for sure $\frac{1}{4}x_i'$ Alice’s key and $\frac{1}{4}y_i'$ Bob’s key and these two parts are not overlapping. If Alice and Bob compare $s$ bit values of their strings $x'$ and $y'$, their chance to detect Eve’s presence is $1-(\frac{2}{3})^s$.

More Details 2.11

c. From the table below, we can see that the chance of $y_i'=x_i'$ is

$\frac{1/8+1/8}{1/8+1/8+1/16+1/16}=\frac{2}{3}$

Therefore, if Alice and Bob compare $s$ bit values of their strings $x'$ and $y'$, their chance to detect Eve’s presence is $1-(\frac{2}{3})^s$.
Only when she measured $\lvert1⟩$ or $\lvert-⟩$, Eve knew for sure Alice’s key. That’s 1/4 chance. Unfortunately, Once Eve measured and sent Bob $\lvert1⟩$ or $\lvert-⟩$, she can’t be sure what Bob’s key is. On the contrary, if Eve measured and sent Bob $\lvert0⟩$ or $\lvert+⟩$, she knew for sure Bob’s key if he didn’t discard his measurement. That’s also 1/4 chance. (See the following table)
Therefore, on average, Eve knew for sure $\frac{1}{4}x_i'$ Alice’s key and $\frac{1}{4}y_i'$ Bob’s key and these two parts are not overlapping.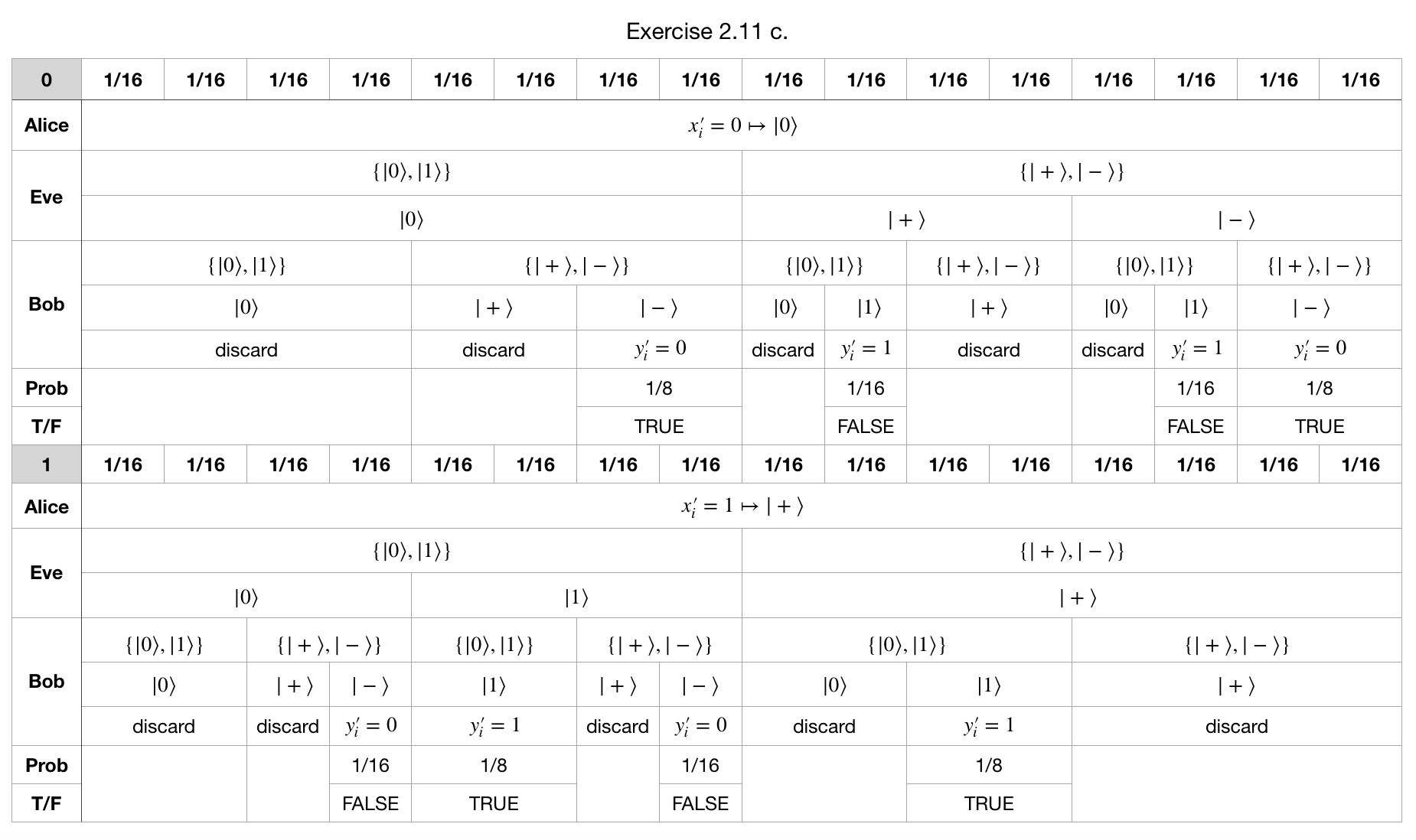

2.7.12 Exercise 2.12

This figure is differet from the text book. (Ref)

Bloch Sphere: Spherical coordinates:
a. Show that the surface of the Bloch sphere can be parametrized in terms of two real-valued parameters, the angles $θ$ and $ϕ$ illustrated in figure 2.7. Make sure your parametrization is in one-to-one correspondence with points on the sphere, and therefore single-qubit quantum states, in the range $θ ∈ [0, π ]$ and $ϕ ∈ [0, 2π ]$ except for the points corresponding to $|0⟩$ and $|1⟩$.
b. What are $θ$ and $ϕ$ for each of the states $|+⟩$, $|-⟩$, $|i⟩$, and $|-i⟩$?

Answer 2.12

a. A point on Bloch sphere can be represented as $(x,y,z)$.
$(θ, ϕ) \mapsto (sinθcosϕ, sinθsinϕ, \cosθ)$
And it’s inverse: $(x,y,z) \mapsto (θ, ϕ)$, where
$θ=\begin{cases} \arctan((x^2+y^2)/{z}) &\text{if } z\ge0\\ π/2-\arctan((x^2+y^2)/{z}) &\text{if } z<0\\ \end{cases}),\spaceϕ=\begin{cases} 0 &\text{if } x=0, y=0\\ \arctan(y/x) &\text{if } x>0, y>0\\ \frac{π}{2} &\text{if } x=0, y>0\\ \arctan(y/x)+π &\text{if } x<0\\ \frac{3π}{2} &\text{if } x=0, y<0\\ \arctan(y/x)+2π &\text{if } x>0, y<0\\ \end{cases}$

Typos

I guess there is a typo here: it should be $ϕ ∈ [0, 2π )$ instead of $ϕ ∈ [0, 2π ]$. Since $ϕ=0$ and $ϕ=2π$ are overlapping. Figure 2.6 (page 24) has another typo: $\lvert0⟩$ should be at the top of the Bloch sphere and $\lvert1⟩$ should be at the bottom. Since $\lvert0⟩ \mapsto (0,0,1)$ and $\lvert1⟩ \mapsto (0,0,-1)$.

b. $\lvert+⟩ \mapsto (1,0,0) \mapsto (\frac{π}{2}, 0),\quad \lvert-⟩ \mapsto (-1,0,0) \mapsto (\frac{π}{2}, π)$
$\quad \lvert i⟩ \mapsto (0,1,0) \mapsto (\frac{π}{2}, \frac{π}{2}),\quad \lvert-i⟩ \mapsto (0,-1,0) \mapsto (\frac{π}{2}, \frac{3π}{2})$

2.7.13 Exercise 2.13

Relate the four parametrizations of the state space of a single qubit to each other:
Give formulas for
a. vectors in ket notation
b. elements of the extended complex plane
c. spherical coordinates for the Bloch sphere (see exercise 2.12)
d. in terms of the $x$, $y$, and $z$ coordinates of the Bloch sphere.

Answer 2.13

It has been shown that:

• $\boxed{a.} \rightleftarrows\boxed{b.}$ (see page 23):
  $a\lvert0⟩+b\lvert0⟩ \mapsto b/a = \alpha$
  and its inverse
  $\alpha= \frac{1}{\sqrt{1+|\alpha|^2}}|0⟩+\frac{\alpha}{\sqrt{1+|\alpha|^2}}|1⟩$.
• $\boxed{b.} \mapsto \boxed{d.}$ (see page 23): if $\alpha=s+it$
  $(s,t) \mapsto (x,y,z)=\left(\frac{2s}{|\alpha|^2+1}, \frac{2t}{|\alpha|^2+1}, \frac{1-|\alpha|^2}{|\alpha|^2+1}\right)$
• $\boxed{c.} \rightleftarrows \boxed{d.}$ (see Exercise 2.12 a.):
  $(θ, ϕ) \mapsto (sinθcosϕ, sinθsinϕ, \cosθ)$
  and it’s inverse
  $(x,y,z) \mapsto (θ, ϕ)$, where
  $θ=\begin{cases}\arctan((x^2+y^2)/{z}) &\text{if } z\ge0\\π/2-\arctan((x^2+y^2)/{z}) &\text{if } z<0\\\end{cases}),\spaceϕ=...$

Let’s figure out $\boxed{d.} \mapsto \boxed{b.}$ and complete the proof. (It has been proved geometricly in “Stereographic projection and Bloch sphere” section 2.5.2. Here is another method.)

• $z=\frac{1-|\alpha|^2}{|\alpha|^2+1} \rArr1+z=\frac{1+|\alpha|^2}{|\alpha|^2+1}+\frac{1-|\alpha|^2}{|\alpha|^2+1}=\frac{2}{|\alpha|^2+1} \rArr \frac{1}{1+z}=\frac{|\alpha|^2+1}{2}$
  $x=\frac{2s}{|\alpha|^2+1} \rArr s=\frac{|\alpha|^2+1}{2}x=\frac{x}{1+z}$
  $y=\frac{2t}{|\alpha|^2+1} \rArr t=\frac{|\alpha|^2+1}{2}y=\frac{y}{1+z}$
  $\therefore \alpha = s + it = \frac{x}{1+z} + i\frac{y}{1+z}$
• $\boxed{d.} \mapsto \boxed{b.}$:
  $(x,y,z) \mapsto \alpha = \frac{x}{1+z} + i\frac{y}{1+z}$

Now we have

$\boxed{a.} \rightleftarrows\boxed{b.} \rightleftarrows\boxed{d.} \rightleftarrows\boxed{c.}$

2.7.14 Exercise 2.14

a. Show that antipodal points on the surface of the Block sphere represent orthogonal states.
b. Show that any two orthogonal states correspond to antipodal points.

Answer 2.14

a. Let’s assume $A=(x,y,z)$ and $A'=(-x,-y,-z)$ are antipodal points on the surface of the Block sphere. From Exercise 2.13, we know
$(x,y,z) \mapsto \alpha = \frac{x}{1+z} + i\frac{y}{1+z} \mapsto |v⟩=\frac{1}{\sqrt{1+|\alpha|^2}}|0⟩+\frac{\alpha}{\sqrt{1+|\alpha|^2}}|1⟩$
$(-x,-y,-z) \mapsto \alpha' = \frac{-x}{1-z} + i\frac{-y}{1-z} \mapsto |v'⟩=\frac{1}{\sqrt{1+|\alpha'|^2}}|0⟩+\frac{\alpha'}{\sqrt{1+|\alpha'|^2}}|1⟩$
$⟨v||v'⟩=\frac{1}{\sqrt{1+|\alpha|^2\sqrt{1+|\alpha'|^2}}}+\frac{\bar{\alpha}\alpha'}{\sqrt{1+|\alpha|^2\sqrt{1+|\alpha'|^2}}}$
$\because\bar{\alpha}\alpha'=\left(\frac{x}{1+z} - i\frac{y}{1+z}\right)\left(\frac{-x}{1-z} + i\frac{-y}{1-z}\right)=\frac{1}{1+z}(x-iy)\frac{1}{1-z}(-x-iy)$
$\enspace\thickspace\qquad=\frac{1}{1-z^2}(-x^2-ixy+ixy-y^2)=\frac{-x^2-y^2}{1-z^2}=\frac{-x^2-y^2}{x^2+y^2}=-1\quad(\because x^2+y^2+z^2=1)$
$\therefore⟨v||v'⟩=0$, i.e. $\{A, A'\}$ represent orthogonal states $\{v, v'\}$.
b. Let’s assume $|v⟩=a|0⟩+b|1⟩$ and $|v'⟩=a'|0⟩+b'|1⟩$ are two orthogonal states. Then
$⟨v||v'⟩= \bar aa'+ \bar bb'=0\rArr \bar aa' =- \bar bb'\rArr \bar a/(-\bar b)=b'/a'\rArr -1/\bar\alpha=\alpha'$
Let’s say $\alpha=s+it$ and $\alpha'=s'+it'$. Then
$-1/\bar\alpha=-\frac{1}{s-it}=-\frac{1}{s^2+t^2}\frac{s^2+t^2}{s-it}=-\frac{1}{s^2+t^2}(s+it)\enspace (\because (s-it)(s+it)=s^2-i^2t^2=s^2+t^2)$
$\therefore -1/\bar\alpha=\alpha' \rArr s'=-\frac{s}{s^2+t^2}=\frac{-s}{|\alpha|^2}$ and $t'=-\frac{t}{s^2+t^2}=\frac{-t}{|\alpha|^2}$
$\therefore |\alpha'|^2=s'^2+t'^2=(\frac{-s}{|\alpha|^2})^2+(\frac{-t}{|\alpha|^2})^2=\frac{s^2+t^2}{|\alpha|^4}=\frac{|\alpha|^2}{|\alpha|^4}=\frac{1}{|\alpha|^2}\rArr |\alpha'|^2|\alpha|^2=1$
From Exercise 2.13, we have
$(s,t) \mapsto (x,y,z)=\left(\frac{2s}{|\alpha|^2+1}, \frac{2t}{|\alpha|^2+1}, \frac{1-|\alpha|^2}{|\alpha|^2+1}\right)$, $(s',t') \mapsto (x',y',z')=\left(\frac{2s'}{|\alpha'|^2+1}, \frac{2t'}{|\alpha'|^2+1}, \frac{1-|\alpha'|^2}{|\alpha'|^2+1}\right)$
$x'=\frac{2s'}{|\alpha'|^2+1}=\frac{2(-s/|\alpha|^2)}{|\alpha'|^2+1}=\frac{-2s}{|\alpha'|^2|\alpha|^2+|\alpha|^2}=\frac{-2s}{1+|\alpha|^2}=-\frac{2s}{|\alpha|^2+1}=-x$
$y'=\frac{2t'}{|\alpha'|^2+1}=\frac{2(-t/|\alpha|^2)}{|\alpha'|^2+1}=\frac{-2t}{|\alpha'|^2|\alpha|^2+|\alpha|^2}=\frac{-2t}{1+|\alpha|^2}=-\frac{2t}{|\alpha|^2+1}=-y$
$z'=\frac{1-|\alpha'|^2}{|\alpha'|^2+1}=\frac{|\alpha'|^2|\alpha|^2-|\alpha'|^2}{|\alpha'|^2+|\alpha'|^2|\alpha|^2}=\frac{|\alpha|^2-1}{1+|\alpha|^2}=-\frac{1-|\alpha|^2}{|\alpha|^2+1}=-z$
$\therefore\{v, v'\}$ correspond to antipodal points $\{(x,y,z), (x',y',z')\}$.